Ziel jeder Regelung ist Ausgangsgröße = Sollwert oder in den Vokabeln der Regelungstechnik Regelgröße = Führungsgröße. Mathematisch wollen wir erreichen, dass y = w gilt. Wir können mit den Regeln des Blockschaltbilds berechnen, wie sich die Regelgröße in Abhängigkeit von der Führungsgröße verhält. Es gilt:
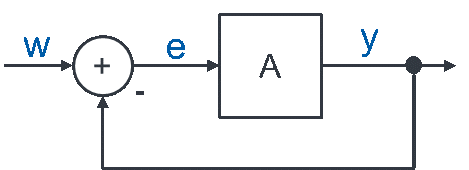
Regelabweichung e = w – y
y = A ∙ e = A ∙ (w – y) = A ∙ w – A ∙ y
Addieren wir auf beiden Seiten der Gleichung den Term A ∙ y, dann gilt
y + A ∙ y = A ∙ w
Wenn y ausgeklammert wird, dann gilt
y ∙ (1 + A) = A ∙ w
Beide Seiten der Gleichung werden durch den Term (1 + A) dividiert:
Das Ziel lautet y = w. Dies ist für A → ∞ erfüllt. Wenn wir im Regler also eine unendlich große Verstärkung realisieren, dann gilt y = w. Das ist in der Praxis nicht realisierbar. Anders ausgedrückt gilt, dass die Regelgröße für große Verstärkungen in der Reihenschaltung aus Regler, Aktor und Strecke ungefähr gleich der Führungsgröße ist. Die Regelabweichung ist dann nur noch sehr gering.
Der Term erreicht für A = 100 etwa den Wert 0,99. Damit ist das Ziel zu 99% erreicht. Die zugehörige Regelabweichung von 1% würde man z. B. bei einem Tempomaten gar nicht bemerken. Bei allen realistischen Werten von A bleibt aber eine Regelabweichung.
Ohne die Formeln zu betrachten wird klar, dass der Ausgang über y = A ∙ e um Faktor A größer ist als die Regelabweichung. Wäre y = w, dann gäbe es keine Regelabweichung mit e = w – y = 0. Mit e = 0 wäre aufgrund von y = A ∙ e = A ∙ 0 auch die Regelgröße y = 0. Ein Regelkreis mit einer Regelgröße ungleich 0 am Ausgang muss also zwingend eine Regelabweichung e aufweisen. Je größer A ist, desto kleiner kann diese ausfallen.
Die Wirkung der Führungsgröße w auf die Regelgröße y wird als „Führungsverhalten“ bezeichnet. Das Führungsverhalten hat die Übertragungsfunktion
Die Führungsgröße w stellt die Eingangsgröße für die Übertragungsfunktion. Die Regelgröße y ist die Ausgangsgröße. Das Ziel y = w wird für HFü = 1 erreicht.
Weiter