Um den Zusammenhang zwischen Spannung und Strom an einem Kondensator bei Wechselstrom zu erklären, greifen wir auf die Analogie des Wassereimers mit Zu- und Ablauf aus Kapitel Energiespeicher zurück. Hier dazu nochmal die Grafik:
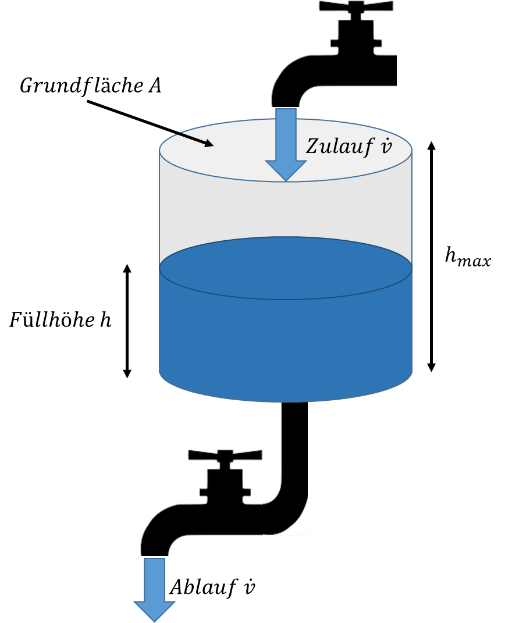
Für die Erklärung von Wechselspannung und Wechselstrom erfolgen Zulauf und Ablauf des Wassers über die Wasserhähne sinusförmig. Damit ändert sich der Füllstand des Eimers sinusförmig.
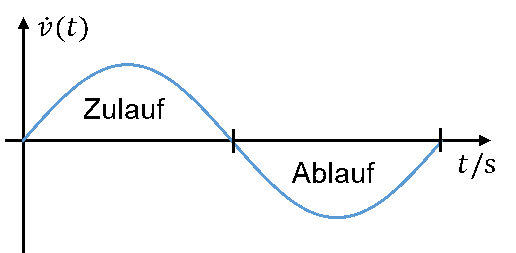
Der Kondensator entspricht in der Analogie dem Eimer. Es gilt:

Wir geben als Eingangsgröße einen sinusförmigen Zulauf vor. Als Ausgangsgröße betrachten wir den resultierenden Füllstand. Am Kondensator bedeutet das: Wir geben den Strom vor und betrachten als Ergebnis bzw. Ausgang die Spannung.
Phasenverschiebung
Wir haben bereits festgestellt, dass der Füllstand immer dann maximal groß ist, wenn der Zulauf positiv war und seinen Nulldurchgang hat, also die Befüllung abgeschlossen ist und die Entleerung beginnt. Während der Zulauf positiv ist, steigt der Füllstand an. So lange der Zulauf negativ ist (also Wasser abläuft), sinkt der Füllstand.
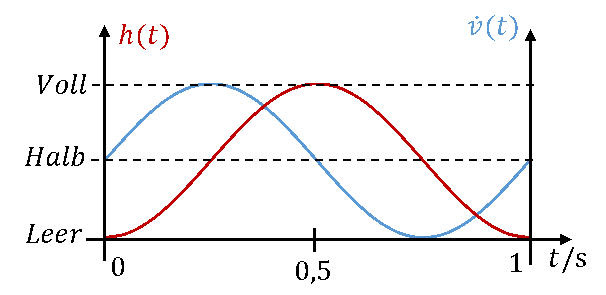
Wenn der Zulauf sinusförmig ist, gibt es eine Phasenverschiebung zwischen Zulauf und Füllstand von einer Viertel-Periode. Der Zulauf ist dem Füllstand zeitlich voraus.
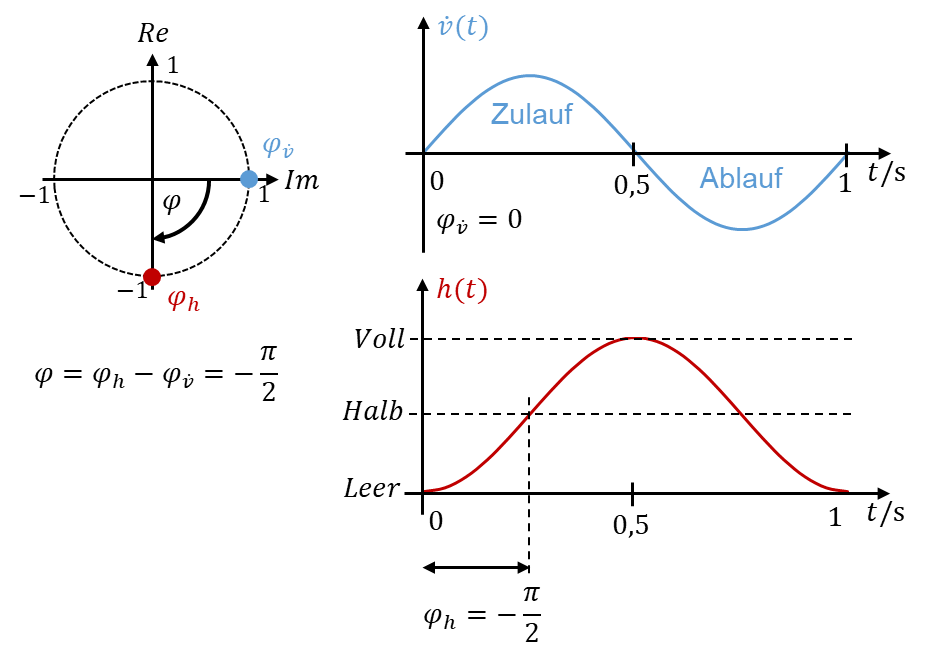
Der Füllstand läuft dem Zulauf hinterher. Wenn der Zulauf keine Phasenverschiebung aufweist, dann ist der Füllstand um φh = -π/2 phasenverschoben.
Jeder Speicher weist eine Phasenverschiebung um ±π/2 zwischen Zulauf und Füllstand auf, wenn sein Zulauf sich sinusförmig ändert. Es gilt auch für Spannung und Strom an den Bauteilen Spule und Kondensator. Sie werden später sehen, dass die Verschiebung einmal +π/2 und einmal – π/2 beträgt.
Die Spannung am Kondensator wird über das Integral des Stroms über der Zeit berechnet. Das Integral über der Zeit bildet die Summe des Stroms in der Vergangenheit ab. Es ist also auch aus der Integration heraus nachvollziehbar, dass ein positiver Strom erst zeitlich verzögert eine positive Spannung zur Folge hat.
Ein Bauelement mit Phasenverschiebung von ±π/2 ist ein dankbarer Glücksfall. Diese Phasenverschiebung können wir mit Multiplikation mit j abdecken:
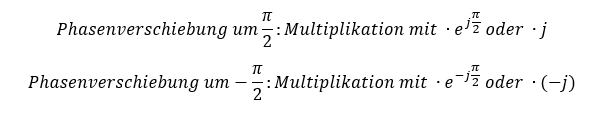
Es gilt für Füllstand und Zulauf am Wassereimer und am Kondensator:
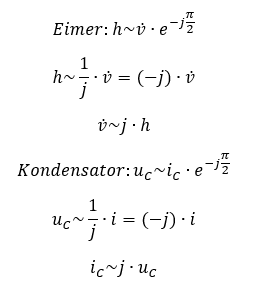
Frequenzabhängigkeit
Betrachten wir als nächstes, wie Zulauf und Füllstand von der Frequenz des Befüllens und Entleerens abhängen. Wird der Eimer mit f = 1Hz befüllt und entleert, dann wird er innerhalb einer Sekunde einmal vollständig befüllt und wieder vollständig geleert.
Wir nehmen jetzt an, dass die Wasserhähne beim Befüllen so weit geöffnet werden, dass Füllstand des Eimers zwischen komplett leer und komplett voll variiert. Jetzt verdoppeln wir die Frequenz des Befüllens. Die Wasserhähne öffnen und schließen wir schneller, aber wir öffnen Sie weiterhin gleich weit wie vorher.
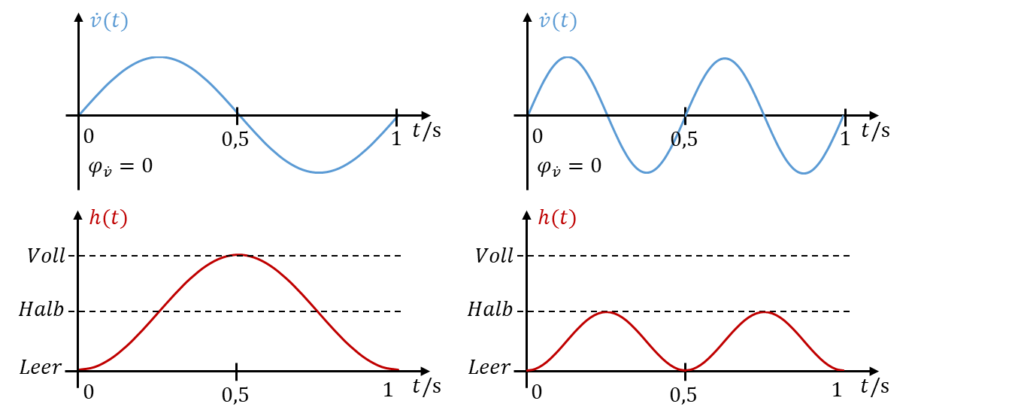
Links oben im Bild sehen Sie das Befüllen und Leeren bei f = 1 Hz, was Sie bereits kennen. Rechts oben wird der gleiche Eimer mit gleichem Spitzenwert und doppelter Frequenz befüllt und geleert. Eine Periode dauert jetzt T = 0,5s lang. Der Vorgang des Befüllens und Leerens ist dann doppelt so schnell vorbei.
Bei f = 2Hz ist nur halb so viel Wasser in den Eimer geflossen. Deshalb steigt der Füllstand auch nur noch auf halbvoll an. Offensichtlich ist der Füllstand abhängig von der Frequenz, wenn wir den Spitzenwert des Zulaufs unverändert lassen. Der Füllstand halbiert sich, wenn die Frequenz verdoppelt wird. Natürlich ist der Füllstand auch weiterhin vom Spitzenwert des Zulaufs abhängig.
Kommen wir vom Wassermodell zur Elektrotechnik. Der Kondensator ist der Eimer. Sein Füllstand ist die Spannung und die Zulaufgeschwindigkeit ist der Strom. Am Kondensator (Eimer) ist die Spannung (Füllhöhe) abhängig davon, wie schnell sich der Strom (Zulaufgeschwindigkeit) ändert. Die Spannung am Kondensator uC ist also umgekehrt proportional zur Frequenz f, mit der sich der Strom iC ändert. Spannung und Strom sind dabei beide sinusförmig, sonst wird es komplizierter. Es gilt:

Bei sinusförmigen Verläufen nutzen wir die Kreisfrequenz ω statt der Frequenz f. Mit ω = 2πf können wir auch schreiben:
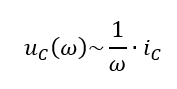
Abhängigkeit von der Fläche
Betrachten wir jetzt zwei Eimer im Vergleich. Sie sind gleich bis auf ihre Grundfläche. Es gilt:
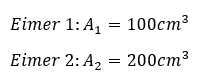
Die gleiche Menge an Wasser führt an Eimer 1 zu einem doppelt so hohen Füllstand wie an Eimer 2. Nehmen wir an, dass die Wasserhähne so weit aufgedreht werden, dass Eimer 1 vollständig gefüllt und geleert wird. Dann sieht das Befüllen folgendermaßen aus:
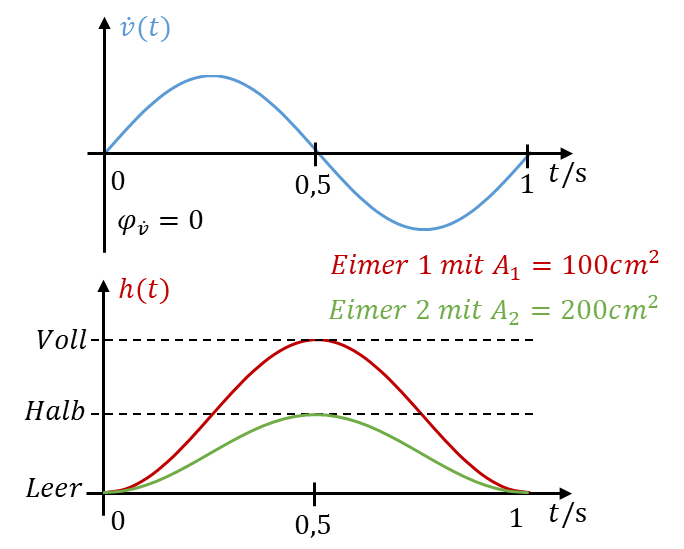
Der Füllstand ist also abhängig von der Grundfläche des Eimers. In der Analogie zur Elektrotechnik ist die Spannung am Kondensator damit abhängig von der Kapazität C des Kondensators. Es gilt

Wir haben damit anschaulich alle Parameter diskutiert, die die komplexe Impedanz eines Kondensators ausmachen. Insgesamt gilt:
