Bei einer Transformation werden die mathematische Beschreibung und oft auch die Sichtweise auf das Signal verändert. Die Laplace-Transformation wechselt vom Zeitbereich, in dem die Signale über der Zeit t als x-Achse aufgetragen sind, in den Frequenzbereich. Hier wird die Frequenz f auf der x-Achse aufgetragen. Die Achse beginnt am Nullpunkt bei f = 0Hz, das entspricht Gleichstrom. Negative Frequenzen machen für in der Elektrotechnik zunächst keinen Sinn. Nach rechts zu hohen Frequenzen hin ist die Achse nicht begrenzt. Je höher die Frequenz f ist, desto weiter rechts liegt der x-Wert der Frequenz in der Abbildung.
Sie kennen einige Frequenzen aus dem Alltag. Die Netzfrequenz der Steckdosenspannung beträgt f = 50Hz. Die Frequenz von WLAN oder Bluetooth beträgt 2,4GHz. Radio empfangen Sie im Bereich [90MHz … 110MHz]. Wenn die Frequenz f auf der x-Achse aufgetragen wird, betrachten wir die Frequenz als veränderlichen Parameter. Wenn sich die Frequenz eines Signals nicht ändert ist das nur praktisch, denn dann betrachten wir nur einen Punkt und nicht mehr einen kontinuierlichen Verlauf wie bei der Zeit.
Im Zeitbereich wird ein Signal mit der Zeit t auf der x-Achse dargestellt. Auf der y-Achse ist die Amplitude dargestellt. Die Amplitude ist der aktuelle Wert, den die Größe zu einem Zeitpunkt t aufweist. Wir können aus einem Zeitverlauf ablesen, welche Amplitude (y-Wert) zu welchem Zeitpunkt (x-Wert) vorliegt. Hier als Beispiel die Spannung an der Steckdose:
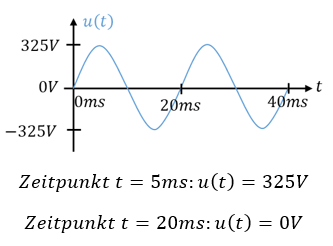
Im Frequenzbereich wird auf der x-Achse die Frequenz f oder die Kreisfrequenz ω aufgetragen. Es gibt zwei y-Werte, einmal den Spitzenwert und dann die Phase. Deshalb werden zwei Grafen gezeichnet, um ein Signal im Frequenzbereich abzubilden. Hier ein Beispiel für die Spannung an der Steckdose, aufgetragen über der Frequenz f:
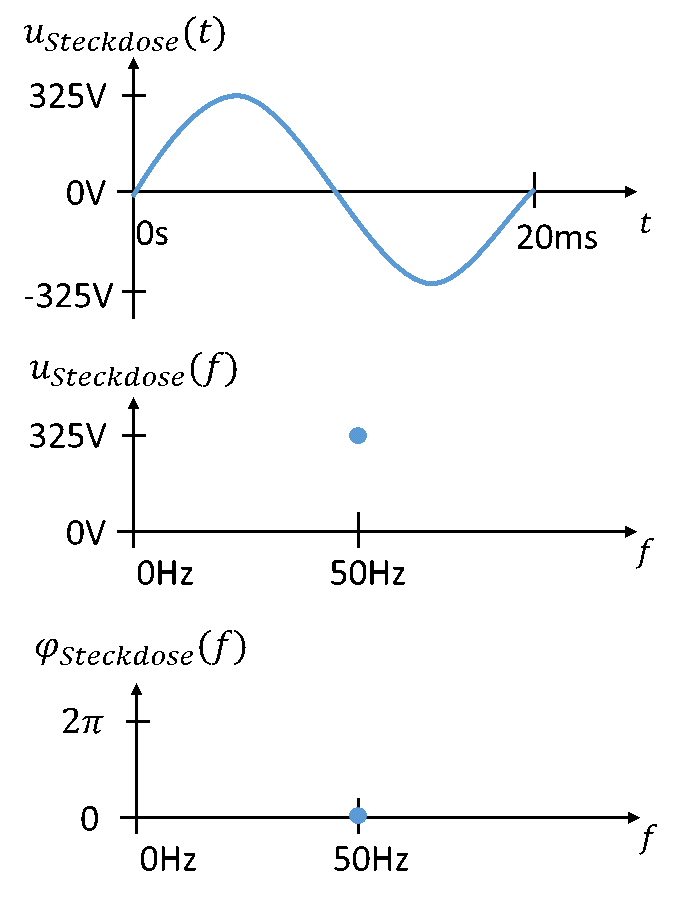
Oben in der Abbildung ist der Spannungsverlauf im Zeitbereich dargestellt. Unten sind die beiden Grafen des Frequenzbereichs dargestellt. Spitzenwert und Phase ergeben nur jeweils einen Punkt, denn die Frequenz an der Steckdose ändert sich nicht. Die Spannung an der Steckdose besteht im „Frequenzbereich“ nur aus einem Spitzenwert und einer zugehörigen Phase. In späteren Vorlesungen werden Sie auch Spannungen kennenlernen, die aus mehreren Teilen zusammengesetzt sind. Wenn die Spannungen unterschiedliche Frequenzen aufweisen, dann gibt es auch mehrere Punkte im Frequenzbereich. Betrachten wir auch dafür ein Beispiel:
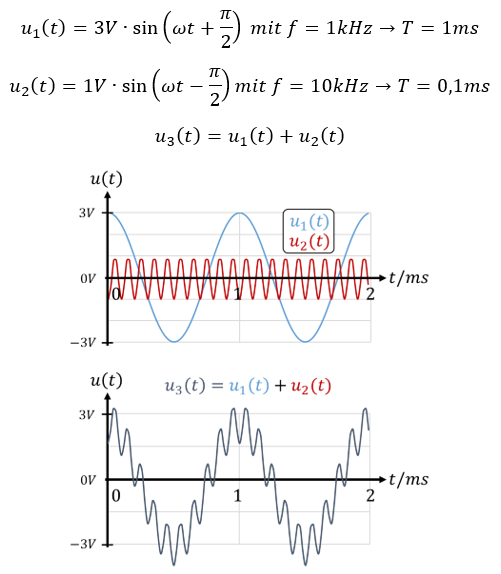
In der oberen Abbildung sehen wir zwei Zeitverläufe von Spannungen. In der hellblauen Spannung u1(t) beträgt die Periodendauer T = 1ms. Das entspricht der Frequenz f = 1kHz. In der roten Spannung u2(t) beträgt die Periodendauer T = 0,1 ms. Das entspricht der Frequenz f = 10kHz. Die Spitzenwerte können wir einfach an der y-Achse ablesen.
In der dunkelblauen Spannung u3(t) sind zwei Frequenzen enthalten. Die Spannung besteht ja aus zwei Teilspannungen (hellblau und rot) mit unterschiedlicher Frequenz. Diese Spannung kann man im Zeitbereich nur schlecht analysieren. Oder erkennen Sie am Zeitverlauf der dunkelblauen Spannung die Parameter der hellblauen und der roten Spannung? Deshalb stellen wir diese Summen-Spannung besser im Frequenzbereich dar:
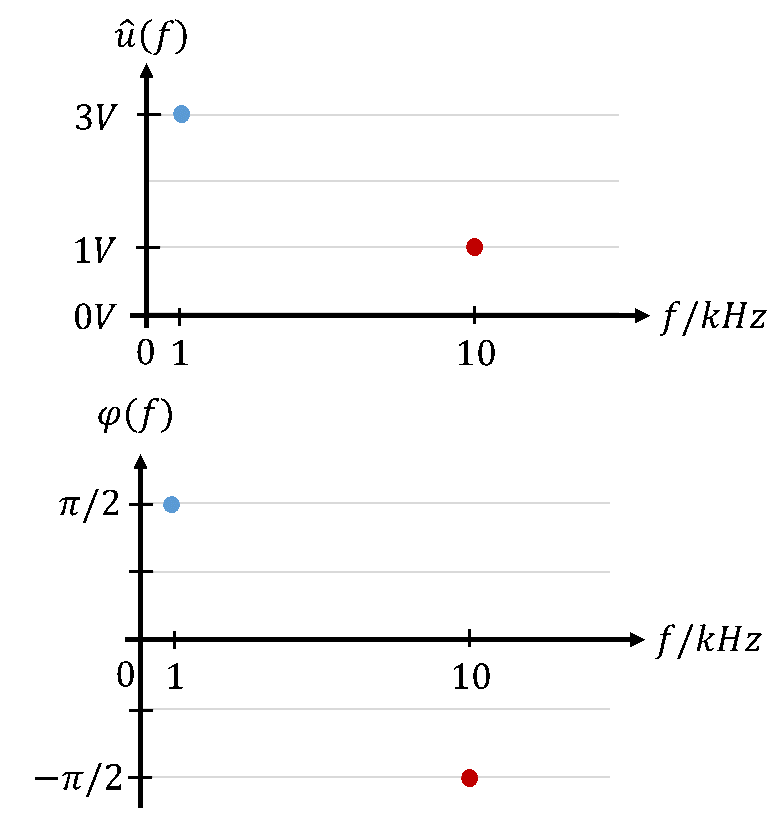
Im oberen Diagramm sind die Spitzenwerte der beiden Spannungen über der Frequenz f als x-Achse dargestellt. Das untere Diagramm zeigt die Phasen beider Spannungen. Jeder Spannung ist im Frequenzbereich ein Spitzenwert und eine Phase zugeordnet. Im Frequenzbereich bekommt jeder Spannungsanteil in einer Summen-Spannung seinen eigenen Punkt für Spitzenwert und Phase. Es ist in dieser Darstellung sehr einfach, die Parameter einer Summen-Spannung direkt abzulesen.
Weiter