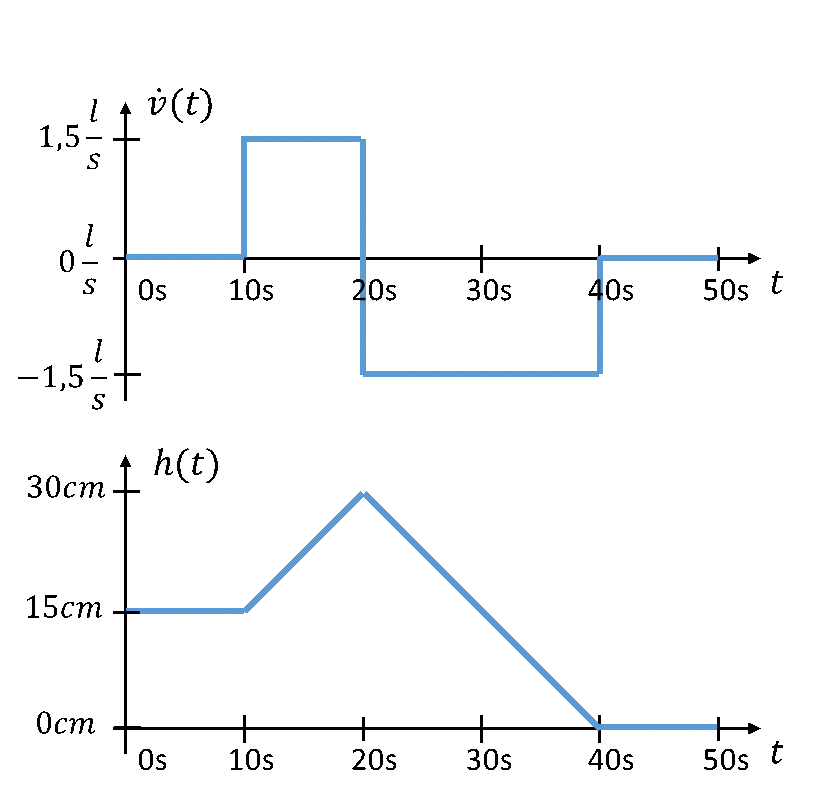
Für diese Zusammenhänge bietet sich eine grafische Betrachtung an: Das Integral eines Zeitverlaufs eines Werts entspricht der Fläche unter dem Zeitverlauf. Das Beispiel wird so erweitert, dass der Füllstand sich 10 Sekunden lang gar nicht ändert, er danach 10 Sekunden lang befüllt wird und nach dem Befüllen 20 Sekunden lang geleert wird.
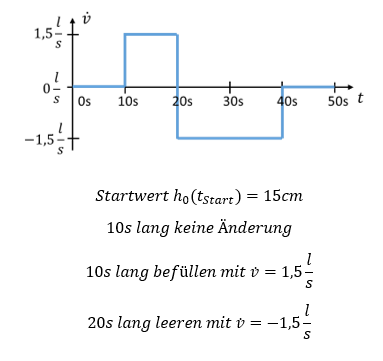
Während der ersten 10 Sekunden ändert sich der Füllstand nicht. Während dieser Zeit benötigen wir offensichtlich keine Berechnung um festzustellen, dass auch zum Zeitpunkt t = 10s der Füllstand noch h = 15cm beträgt.
Für die grafische Lösung der Integrale werden die Flächen unter dem Grafen der Befüllung über der Zeit bestimmt. Es gilt: Das Integral entspricht dem Flächeninhalt des Verlaufs, der integriert wird.
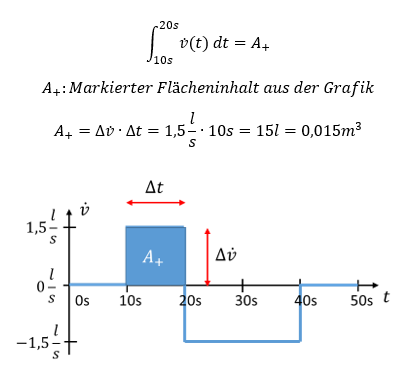
Nach 10 Sekunden erfolgt der Füllvorgang. Das Integral wird in der Formel durch die Fläche ersetzt. Es gilt:
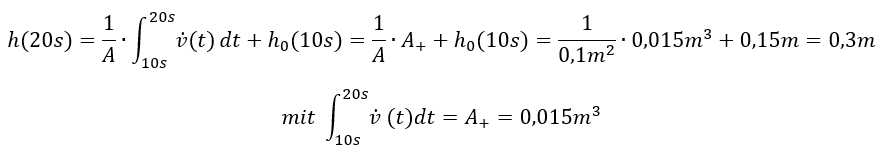
Die Einheit der Fläche im Verlauf des Füllvorgangs hat i. A. nicht die Einheit Quadratmeter. Es handelt sich um einen Rechentrick zur Vereinfachung der Integralrechnung. Die Einheiten müssen Sie dafür ausblenden. Die Einheit dieser „Fläche“ ist das Produkt der Einheiten an beiden Achsen (hier l/s und s).
Das Ergebnis mit Hilfe der Flächenberechnung entspricht dem mit Hilfe der Stammfunktion. Das zeigt exemplarisch, dass das Verfahren mit Hilfe der Fläche zulässig ist. Oft sind Flächen leichter als Stammfunktionen zu bestimmen. Diese Flächen sind natürlich nicht immer Rechtecke. Über die Fläche können Sie auch Integrale sehr komplexer Funktionen bestimmen. Das Verfahren bietet vor allem bei realen Messverläufen Vorteile, wenn Sie eine Abschätzung über das Integral über dem Kurvenverlauf brauchen.
Setzen wir das Verfahren für den Leerungs-Vorgang ein:
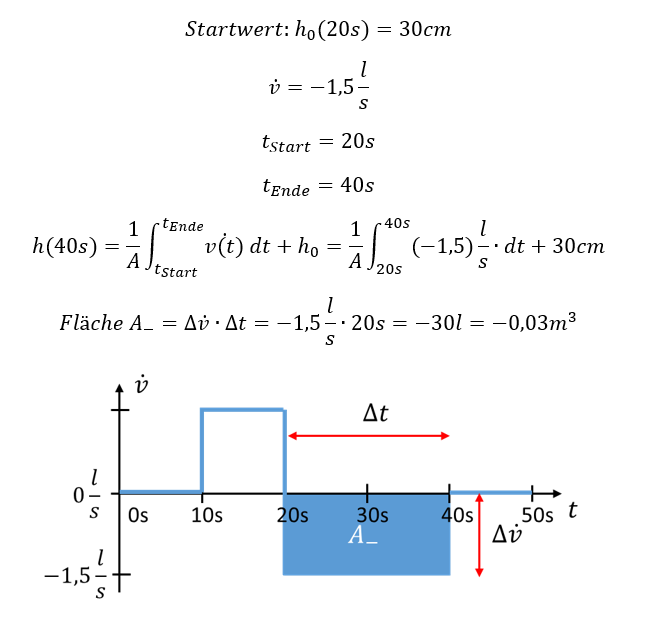
Damit gilt für den Füllstand zum Zeitpunkt t = 40s:
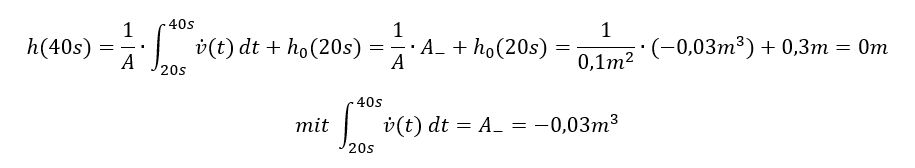
Am Ende ist der Eimer leer. Bei der Betrachtung des Leerens des Eimers wird in der Grafik direkt deutlich, dass die Fläche unterhalb der Zeitachse doppelt so groß ist wie die Fläche oberhalb der Zeitachse. Der Eimer wird um doppelt so viel Wasser entleert wie er vorher aufgefüllt wurde.
Während der Zeitbereiche, in denen weder Zu- noch Ablauf erfolgen, ändert sich der Füllstand nicht.
Bisher haben wir den Füllstand zu festen Zeitpunkten ausgerechnet. Der Verlauf zwischen diesen Zeitpunkten ist bei konstanter Befüllung linear.
Das anschauliche Beispiel des Eimers wird im folgenden Kapitel für die Erklärung des Verhaltens elektrischer Speicher genutzt.
Weiter