Betrachten wir Spannungen und Ströme als komplexe Zahlen. Dabei ändern wir zwei Parameter. Zunächst ist es für die Berechnung von Wechselspannungsnetzwerken hilfreich, als Parameter auf der x-Achse die Kreisfrequenz ω statt der Frequenz f zu wählen. Der Vorteil erschließt sich erst, wenn wir in ein paar Kapiteln Speicher bei Wechselstrom betrachten. Wir multiplizieren beim Umrechnen von f in ω einfach nur mit dem Faktor 2π. Es gilt ω = 2πf.
Dann ändern wir die Winkelschreibweise von DEG (das mit °) in RAD (das mit π). Für die Umrechnung nutzen Sie bitte folgende Darstellung:
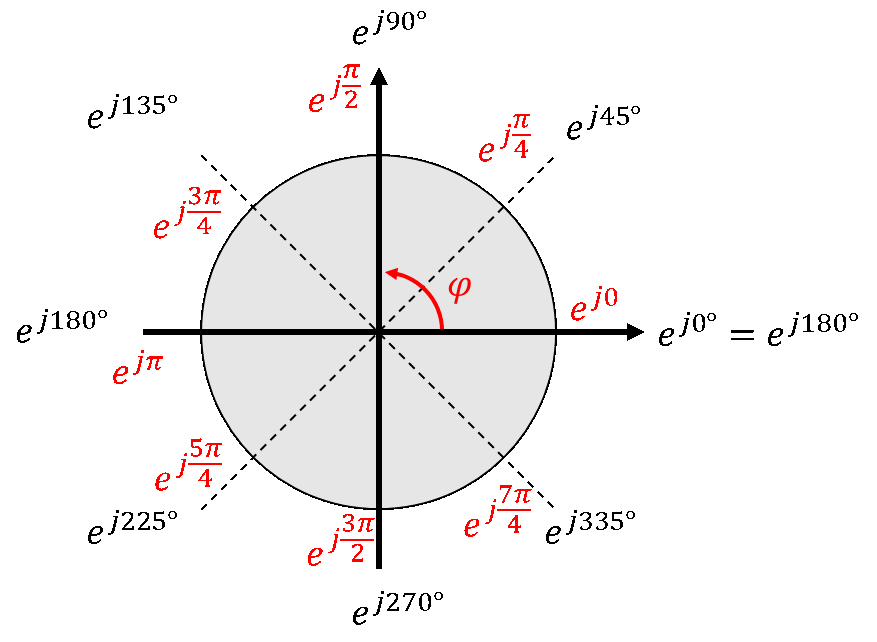
Bitte stellen Sie Ihren Taschenrechner auf RAD um, sonst sind alle Ihre Ergebnisse falsch. Das Rechnen mit RAD statt DEG ist eine beliebige Konvention, Sie können natürlich auch alles in DEG rechnen. Man muss sich für eine Winkeldarstellung entscheiden, und ich habe mich für RAD entschieden. Es hat meiner Meinung nach weder Vor- noch Nachteile.
Zunächst formen wir Beispiel-Spannungsverläufe aus dem Zeitbereich u(t) in komplexe Zahlen u(ω) um. Es gilt:
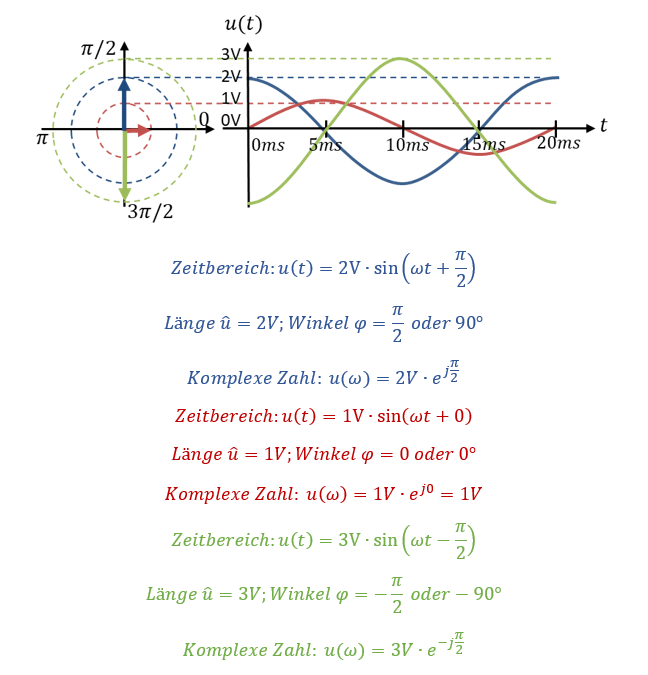
Komplexe Zahlen werden in der Elektrotechnik oft mit einem Unterstrich versehen. Eigentlich müssen alle komplexen Spannungen, Ströme etc. immer mit einem Unterstrich versehen werden. Sonst könnte eine Gleichspannung nicht von einer rein reellen sinusförmigen Spannung unterschieden werden, die beide den gleichen Spitzenwert aufweisen. In diesem Kapitel geht es aber nur um Wechselstrom, deshalb spare ich mir dies aus Faulheit. Wechselgrößen nutzen kleine Buchstaben und Gleichgrößen nutzen Großbuchstaben. Das muss ausreichen.
Übung
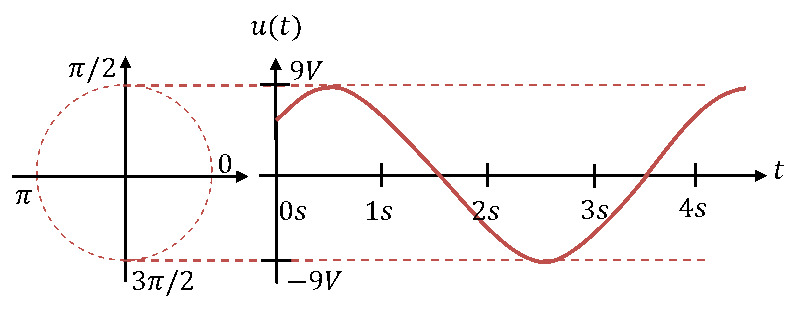
a) Bestimmen Sie die Parameter Spitzenwert, Periodendauer, Frequenz, Kreisfrequenz und Phasenwinkel der Spannung u(t).
b) Beschreiben Sie die Spannung mathematisch im Zeitbereich.
c) Beschreiben Sie die Spannung im Frequenzbereich in Exponentialform und in Normalform.
d) Zeichnen Sie den Vektor, der Spitzenwert und Winkel angibt, in den Kreis im linken Teil der Abbildung ein.
e) Zeichnen Sie Spitzenwert und Phase in ein Diagramm ein, in dem beide Größen jeweils über der Frequenz aufgetragen sind.
Lösung:
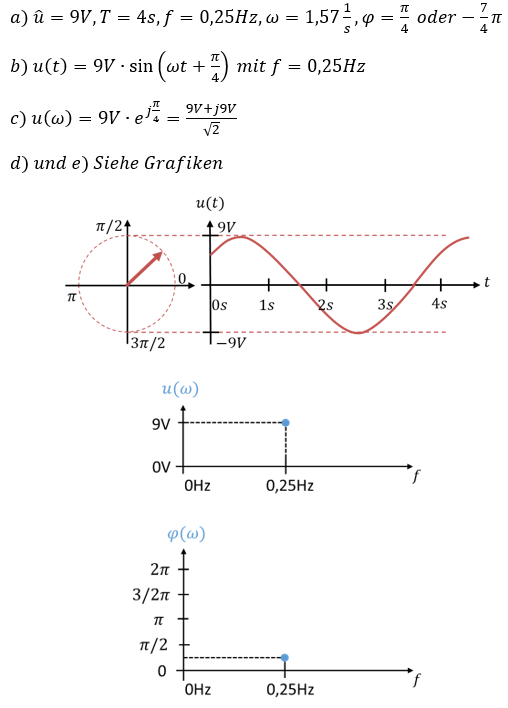
Typische Drehoperatoren
Wenn wir Drehoperatoren in Expontentialform schreiben, dann weisen sie automatisch die Länge 1 auf. Wenn wir Richtungen in Komponentenform beschreiben, müssen wir daraus zuerst einen normierten Richtungsvektor der Länge 1 bauen.
Die Richtung 0° zeigt in der komplexen Ebene nach rechts. Damit beschreibt der Drehoperator ej0 auf der Reellen Achse auf die +1. Die Richtungen der 4 Hauptachsen können wir relativ leicht als Richtungsvektoren angeben:

Die Winkelhalbierenden dazwischen können wir ebenfalls in Komponentenform angeben. Betrachten wir dafür eine Drehung um den Winkel 45° bzw. π/4:
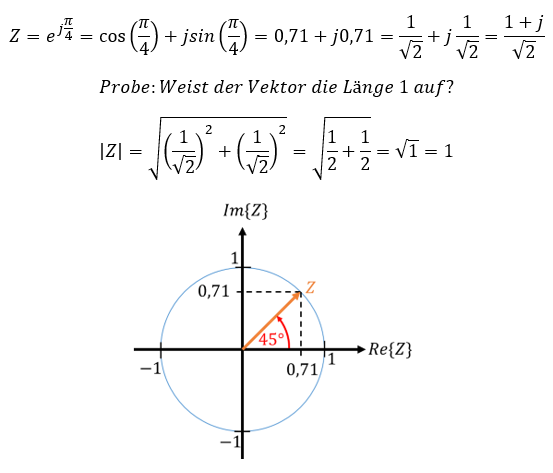
Wir bauen den Richtungsvektor aus einem positiven Realteil und einem positiven Imaginärteil auf. Real- und Imaginärteil sind kleiner als die Länge des Vektors.
Andere Winkelhalbierende konstruieren wir nach einem ähnlichen Schema:
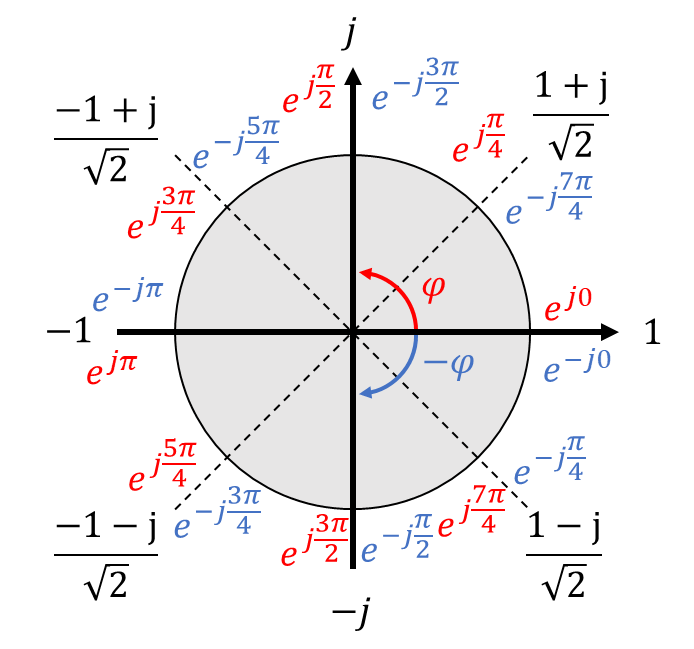
In der oberen Darstellung sind verschiedene Darstellungsformen typischer Winkel enthalten. In schwarz sind die Winkel in Komponentenform angegeben. In rot sind die Winkel als RAD in positiver Richtung angegeben. Wenn wir das Vorzeichen im Exponenten rumdrehen, laufen wir den Kreis im Uhrzeigersinn entlang. Dann ergeben sich die blauen Schreibweisen. Alle Schreibweisen bilden die gleichen 8 Winkel ab.
Multiplikation mit j
In der komplexen Wechselstromrechnung mit Speichern (später) multiplizieren wir oft Terme mit j oder mit -j. Eine Multiplikation mit j dreht einen Vektor um 90° oder π/2 gegen den Uhrzeigersinn. Eine Multiplikation mit -j dreht einen Vektor um 90° oder π/2 im den Uhrzeigersinn. Diese Multiplikationen sind reine Drehoperationen, denn die Länge der Operatoren ist jeweils 1. Sie ändern also nicht die Vektorlänge.
Eine Multiplikation mit j∙j dreht zweimal um π/2, also insgesamt um den Winkel π. Wenn ich bei φ = 0 (also bei +1 auf der reellen Achse) starte und um den Winkel π drehe, lande ich am Punkt -1 auf der reellen Achse. Die Aussage der Mathematiker, dass j∙j=-1 gilt, kann mit diesen Drehungen leicht nachvollzogen werden.
In der folgenden Abbildung gilt ublau=j ∙ 2 ∙ urot. Der Spitzenwert der blauen Kurve ist um Faktor 2 höher als der der roten Kurve. Die Phase des blauen Verlaufs ist um π/2 nach „links“ verschoben. Das entspricht einer Multiplikation mit dem Faktor j.
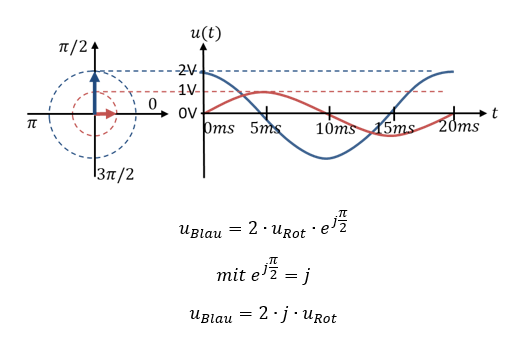
Weiter