Schaltungen mit Ohm´schen Verbrauchern und Speichern benötigen i. A. Wirkleistung und Blindleistung. Die Wirkleistung wandelt die elektrische Energie an den Ohm´schen Verbrauchern in andere Energieformen um. Die Blindleistung schiebt elektrische Energie zwischen Speichern wie Spulen und Kondensatoren hin- und her. Die Scheinleistung ist die Summe beider Leistungsarten.
Die Zeitverläufe aus dem letzten Kapitel helfen beim Verstehen der beiden Leistungsarten. Für die Berechnung wechseln wir wieder zu komplexen Zahlen. Wirkleistung ist rein reell. Blindleistung ist rein imaginär. Deshalb wird die komplexe Scheinleistung folgendermaßen definiert:

Die Berechnung von Wirk- und Blindleistung aus der Scheinleistung erfolgt über den Phasenwinkel φ. Er wird aus der Differenz der Spannungsphase und der Stromphase berechnet.
Die Scheinleistung s wird in der komplexen Wechselstromrechnung als s(ω) = u(ω) ∙ i(ω)* berechnet. Der Stern steht für den mathematischen Operator „konjugiert komplex“. Bei einer konjugiert-komplexen Zahl wird das Vorzeichen des Imaginärteils umgedreht. Es gilt z. B. (1+j)* = 1-j. Die Wirkleistung p(ω) ist dann als Realteil der Scheinleistung und die Blindleistung q(ω) als Imaginärteil der Scheinleistung definiert. Es gilt also s = p + jq.
Leider sind unterschiedliche Einheiten für die drei Typen der Leistung definiert. Die Scheinleistung s wird in der Einheit [s] = V ∙ A angegeben. Die Blindleistung q hat die Einheit [q] = var und die Wirkleistung die bekannte Einheit [p] = W.
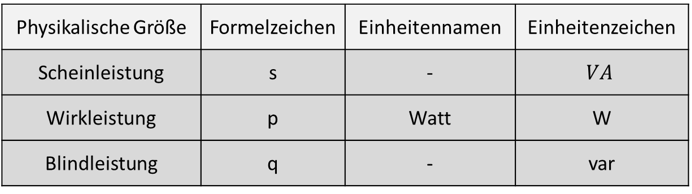
Wir betrachten als Beispiel eine Spannung u(ω) = j3V und einen Strom i(ω) = 2A – j2A.
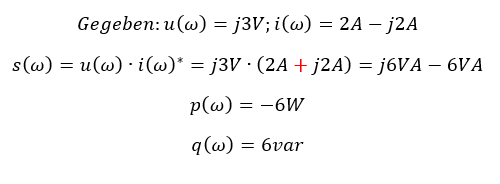
Die Blindleistung q wird immer ohne das j angegeben. Das j steckt in der Gleichung s = p + jq. Deshalb sind p und q reell. Die unterschiedlichen Einheiten haben den Sinn, direkt kenntlich zu machen, welche Art von Leistung vorhanden ist. So lange wir eine Scheinleistung s angeben, ist die Einheit immer VA. Erst wenn wir dann p oder q angeben, können wir die Einheiten W oder var verwenden.
An einem Ohm´schen Widerstand kann es nur Wirkleistung geben. An einem Speicher nur Blindleistung. Die Blindleistung an einer Spule ist immer positiv, die an einem Kondensator immer negativ. Das werden Sie beim Rechnen von Aufgaben selbst feststellen. Es ist für die Kontrolle der Ergebnisse hilfreich das zu wissen.
Leistungsfaktor
Wenn Sie z. B. elektrische Anlagen betreiben, wollen Sie i. A. möglichst viel Wirkleistung erzielen. Blindleistung ist i. A. unerwünscht, denn sie bewirkt in der Anlage nichts, über sie werden nur Speicher umgeladen. Wie kann der Anteil der Wirkleistung an der Scheinleistung in der Praxis einfach bestimmt werden um zu prüfen, wie „gut“ Ihre Anlage ist? Dafür nutzen wir den Leistungsfaktor.
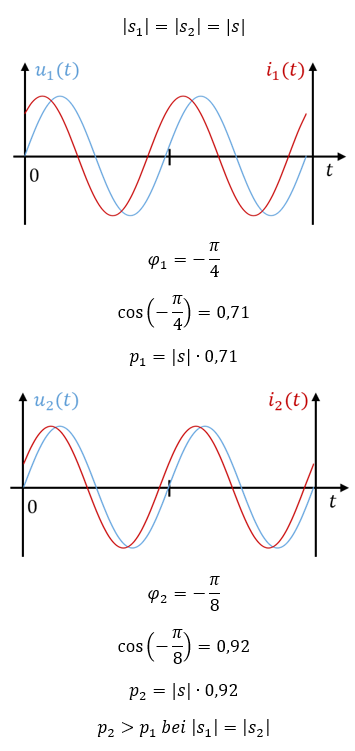
Der Winkel φ ist in der oberen Abbildung zwischen der reellen Achse (x-Achse) und dem Zeiger (Vektor) der Scheinleistung eingezeichnet. Er beschreibt am Dreieck, wie sich die Scheinleistung in Wirk- und Blindleistung aufteilt. Der Anteil der Wirkleistung p an der Scheinleistung s wird durch den Leistungsfaktor cos(φ) ausgedrückt. Eine „gute“ Anlage mit wenig Blindleistung weist einen Leistungsfaktor von cos(φ) = 1 auf.
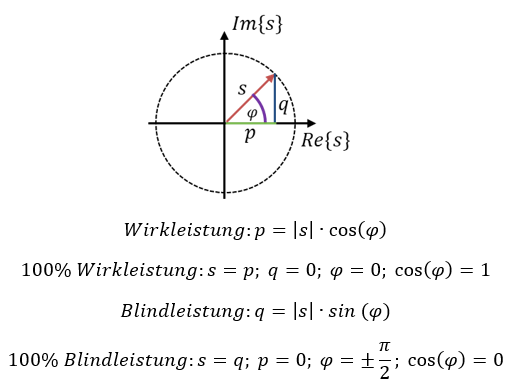
Der Winkel φ der Leistung entspricht der Phasenverschiebung φ zwischen Spannung und Strom. Das zeige ich Ihnen an folgendem Beispiel:
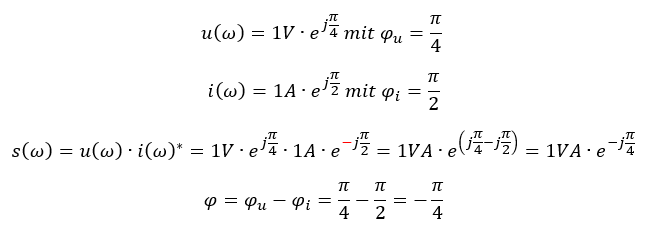
Sie können also auf die Wirkleistung schließen, indem Sie die Zeitverläufe von Spannung und Strom analysieren. Die Phasenverschiebung zwischen Spannung und Strom können Sie aus dem zeitlichen Abstand der positiven Nulldurchgänge der Verläufe ermitteln. Sie müssen diese Zeit in Relation zur Periodendauer setzen. Das Verfahren zur Bestimmung des Phasenwinkels ist in diesem Kapitel erklärt.
Anschließend ermitteln Sie die Spitzenwerte von Spannung und Strom und multiplizieren diese zum Spitzenwert der Scheinleistung. Dieser Spitzenwert multipliziert mit cos(φ) ergibt den Spitzenwert der Wirkleistung.
Es folgen zwei Abbildungen von Spannungs- und Stromverläufen. Die Spitzenwerte von Spannung und Strom sind in beiden Verläufen gleich groß. Deshalb ist auch der Betrag der Scheinleistung in beiden Verläufen gleich groß. Der zeitliche Abstand zwischen Spannung und Strom ist proportional zu deren Phasenverschiebung. Der Phasenwinkel der oberen Verläufe ist größer als der der unteren Verläufe. Der Anteil der Wirkleistung an der Scheinleistung ist um unteren Verlauf größer als im oberen Verlauf.
Beispiel einer Schaltung
Betrachten wir die Leistung, die die Spannungsquelle in der unteren Abbildung abgibt.
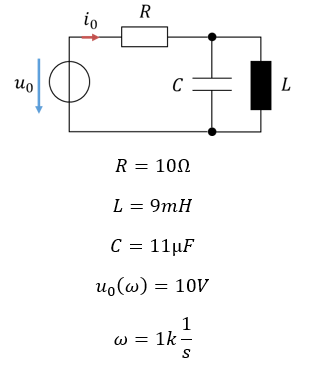
Zunächst berechnen wir den Strom, der aus der Quelle fließt. Dafür wird die Gesamtimpedanz der Last ZGes gebildet:

Betrachten wir die Phasenwinkel:
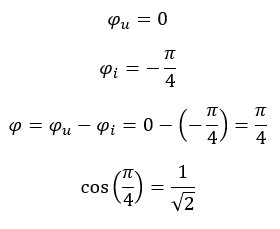
Das ist auch der Phasenwinkel der Scheinleistung. Die Wirkleistung entspricht der Leistung am Widerstand, denn an Spule und Kondensator fällt nur Blindleistung an. Es gilt:
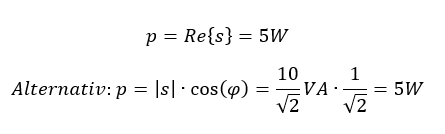
Effektive Leistung
Komplexe Größen bilden in der Elektrotechnik immer Spitzenwerte und Phase ab. Der Spitzenwert ist aber kein gutes Maß für die Leistung, siehe Kapitel Mittelwert und Effektivwert. Niemanden in der Praxis interessiert die Wirkleistung als Spitzenwert. Wenn wir wissen wollen, wie heiß ein Fön wird, dann brauchen wir immer die effektive Wirkleistung. Die effektive komplexe Scheinleistung erhalten wir, wenn wir Spannung und Strom jeweils als Effektivwert einsetzen. Es gilt für sinusförmige Spannungen und Ströme:
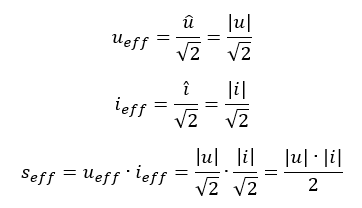
Der Effektivwert ist eine reelle Zahl, keine komplexe Zahl. Er beinhaltet keinen Winkel, es ist also kein Vektor. Er kennt deshalb auch keinen Real- oder Imaginärteil. Wir können deshalb auch den effektiven Strom nicht konjugiert komplex betrachten. Wenn wir die Scheinleistung als Spitzenwert ermittelt haben, dann können wir die effektive Scheinleistung einfach mit folgender Formel berechnen:
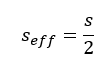
Die effektive Scheinleistung ist halb so groß wie der Spitzenwert der Scheinleistung. Das liegt daran, dass die Spitzenwerte von Spannung und Strom jeweils durch Wurzel (2) geteilt worden sind.
Rechnen mit Scheinleistung in Netzwerken
Angenommen Sie haben die Scheinleistung aller Bauelemente in einer Schaltung aus deren Spannungs- und Stromwerten ermittelt. Wie können Sie die gesamte Scheinleistung der Schaltung ermitteln? Dafür gibt es zwei Wege.
Sie können die Scheinleistung der Quelle berechnen. Dazu nutzen Sie Spannung und Strom an der Quelle und rechnen genauso wie an passiven Bauelementen.
Alternativ können Sie Scheinleistungen addieren. Betrachten wir dazu zunächst eine Reihenschaltung aus zwei Bauelementen. Als Beispiel verwende ich in den Grafiken Widerstände, die Zusammenhänge gelten aber für alle Arten von Bauelementen. Der Strom durch beide Bauelemente ist gleich groß. Die Spannungen werden zu einer Gesamtspannung addiert. Die gesamte Scheinleistung der beiden Bauelemente ergibt sich damit aus der Addition der einzelnen Scheinleistungen. Es gilt:
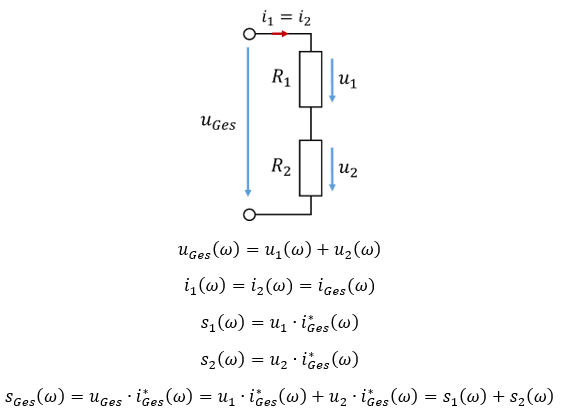
In einer Reihenschaltung addieren sich die Scheinleistungen der Bauelemente zu einer Gesamtschaltung.
Betrachten wir als nächstes eine Parallelschaltung:
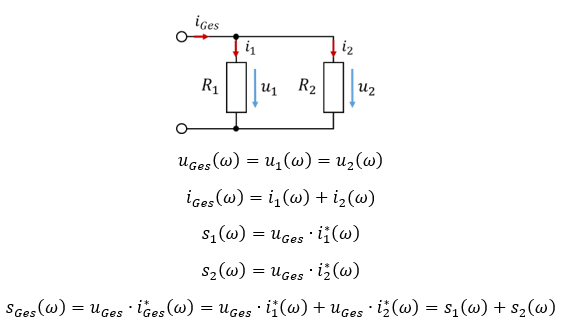
Auch die Gesamtscheinleistung von zwei parallel geschalteten Bauelementen entspricht ebenfalls der Summe der Scheinleistungen der Bauelemente.
Bei der Reihenschaltung ist der Strom in beiden Bauelementen gleich groß und die Spannungen beider Bauelemente werden addiert. Bei der Parallelschaltung ist die Spannung in beiden Bauelementen gleich groß und die Ströme beider Bauelemente werden addiert. Beides führt dazu, dass die Scheinleistungen der Bauelemente zur Gesamtscheinleistung addiert werden.
Es ist offenbar egal, wie Bauelemente verschaltet sind. Sie können immer die Scheinleistungen aller Bauelemente addieren und erhalten die Gesamtscheinleistung der Schaltung.
Zusammenfassung
Wenn wir Spannung und Strom im Zeitbereich messen und miteinander multiplizieren, erhalten wir immer die Scheinleistung. Der Mittelwert der Scheinleistung s(t) im Zeitbereich entspricht dem Mittelwert der Wirkleistung p(t). Der Anteil der Scheinleistung, der mittelwertfrei sinusförmig um die x-Achse schwingt ist die Blindleistung q(t). Im Zeitbereich sind diese Größen schwierig zu messen.
Wir betrachten die komplexen Größen u(ω) und i(ω)*. Wenn wir diese miteinander multiplizieren und wir erhalten die komplexe Scheinleistung s(ω). Der Realteil der Scheinleistung entspricht der Wirkleistung p(ω), der Imaginärteil der Blindleistung q(ω). Liegt die Scheinleistung als komplexe Zahl in Normalform vor, können Sie also Wirk- und Blindanteil aus s(ω) = p(ω) + jq(ω) einfach ablesen.
Den Anteil der Wirkleistung an der Blindleistung erhalten wir aus dem cos(φ) = q(ω) / s(ω). Der Winkel φ entspricht der Phasenverschiebung zwischen Spannung und Strom.
Weiter