Sie kennen ganze Zahlen. Das sind Zahlen ohne Komma, also Zahlen wie -6, 0, 120 oder 1000. Mit diesen Zahlen rechnen wir in der Grundschule. Dann gibt es rationale Zahlen. Sie füllen die Zwischenräume aus. Beispiele für rationale Zahlen sind 0,175 oder 3,5. Die rationalen Zahlen können positiv oder negativ sein. Sie sind auf einem Zahlenstrahl angeordnet. Je weiter wir am Zahlenstrahl nach rechts laufen, desto größer werden die Zahlen.
Wir können eine Ebene aus zwei rationalen Zahlenstrahlen aufspannen. Die eine Richtung nennen wir x, die andere y. Das ist die Ebene, in der Sie Vektorrechnung kennengelernt haben. Sie haben dabei zwei rationale Zahlen einfach orthogonal zueinander gesetzt. Mit zwei Zahlen – der x-Komponente und der y-Komponente – beschreiben Sie jetzt die Lage eines Punkts in der Ebene.
Komplexe Zahlen erweitern die rationalen Zahlen sehr ähnlich wie die x-y-Ebene. Eine komplexe Zahl besteht aus zwei Zahlen, ähnlich wie die Koordinaten eines Punkts in der Ebene. Nur benennen wir die Richtungen nicht als x und y, sondern als reelle Achse und als imaginäre Achse. Beide Achsen sind Zahlenstrahlen aus reellen Zahlen zwischen -∞ und +∞ mit der 0 in der Mitte. Die Zahl auf der imaginären Achse bekommt aber einen Vorfaktor: Das i bzw. das j.
Die Bedeutung von „j“
Die Mathematiker definieren i als die Wurzel aus -1. In der Schule haben Sie gelernt, dass für negative Zahlen keine Wurzel definiert ist. Das ist genauso wenig richtig, wie dass es nur ganze Zahlen gibt. Für die Zwischenwerte hatten wir die rationalen Zahlen definiert. Als Wurzel aus -1 definieren die Mathematiker die Zahl i. Sie können die Wurzel aus anderen negativen Zahlen durch das i ausdrücken.
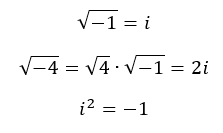
Komplexe Zahlen bestehen aus einer reellen Zahl und einer imaginären Zahl. Ein Beispiel ist die komplexe Zahl Z = 3 + i2.
In der Elektrotechnik nutzen wir komplexe Zahlen für sehr viele Anwendungen. Der Buchstabe „i“ der Mathematiker ist bei uns mit dem Strom besetzt. Deshalb verwenden wir in der Elektrotechnik immer den Buchstaben „j“ an Stelle von „i“ für die Wurzel aus -1. Eine komplexe Zahl sieht in der Elektrotechnik also so aus: Z = 3 + j2.
Der Realteil einer komplexen Zahl ist der Wert auf der reellen Achse. Im Beispiel der Zahl Z = 3 + j2 ist der Wert 3 der Realteil. Es ist die Zahl ohne j. Der Imaginärteil ist der Wert auf der imaginären Achse. Im Beispiel Z = 3+j2 ist 2 der Imaginärteil. Wir schreiben den Imaginärteil als reelle Zahl, also ohne das j. Das j wird bei der imaginären Zahl mitgedacht. Es gehört zur Achse, nicht zur Zahl.
Die komplexe Ebene
In der komplexen Ebene werden komplexe Zahlen grafisch dargestellt. Die reelle Achse zeigt in Richtung der x-Achse aus der Vektorrechnung. Die imaginäre Achse zeigt in Richtung der y-Achse. Komplexe Zahlen sind Punkte in der komplexen Ebene. Betrachten wir ein paar Beispiele:
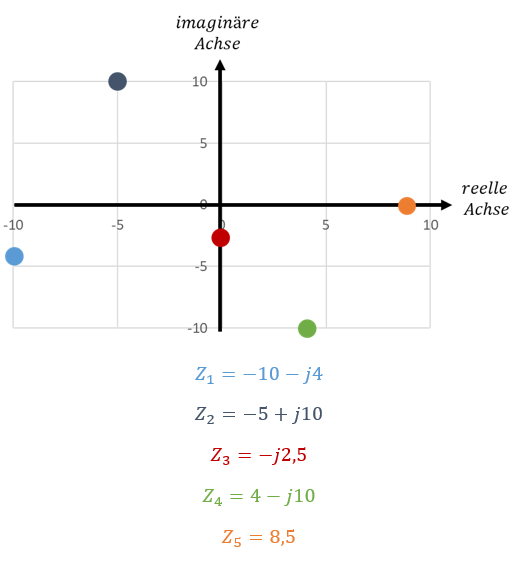
Eine rein reelle Zahl ist ein Spezialfall einer komplexen Zahl mit Imaginärteil 0 (orange). Eine rein imaginäre Zahl hat einen Realteil von 0 (rot). Als Konvention schreiben wir den Realteil zuerst und dahinter den Imaginärteil.
Weiter