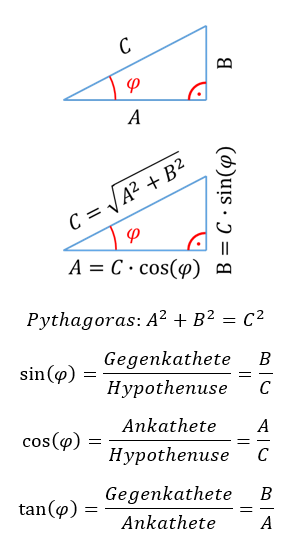
Für die folgende Überlegung brauchen wir Dreiecksmathematik. Deshalb hier eine kurze Auffrischung. In einem rechtwinkligen Dreieck mit den Seitenlängen A, B und C gelten folgende Rechenregeln:
Wir können eine komplexe Zahl in der komplexen Ebene als Punkt darstellen. Alternativ können wir sie als Zeiger (Pfeil) vom Ursprung des Koordinatensystems zum Punkt darstellen. Dieser Pfeil hat eine Länge und eine Richtung. Die Richtung wird als Winkel angegeben. Der Nullpunkt des Winkels ist die Richtung der reellen Achse (nach rechts). Die Länge berechnen wir aus Realteil und Imaginärteil. Der Pfeil bildet immer ein rechtwinkliges Dreieck mit der reellen Achse, an dem wir mit Sinus und Cosinus rechnen können. Betrachten wir die (grüne) komplexe Zahl aus dem Beispiel oben:
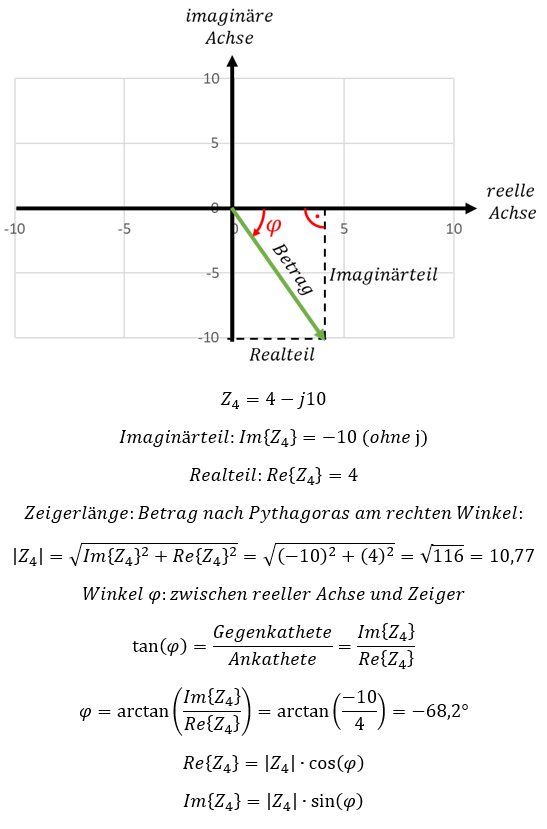
Wir kürzen „Imaginärteil“ mit Im{…} und „Realteil“ mit Re{…} ab. Der Winkel φ wird gegen den Uhrzeigersinn positiv eingezeichnet. Der Winkel φ = 45° zeigt also nach oben rechts. Im Beispiel oben ist der Winkel negativ, weil er von der reellen Achse aus betrachtet gegen den Uhrzeigersinn gezeichnet ist.
Eine komplexe Zahl können wir auf zwei Arten mathematisch beschreiben: Entweder geben wir Realteil + j Imaginärteil an. Dann wandern wir den Realteil in Richtung der reellen Achse und den Imaginärteil in Richtung der imaginären Achse entlang und erreichen so den Punkt in der komplexen Ebene. Diese Form der mathematischen Beschreibung bezeichnen wir als Komponentenform.
Oder wir geben den Betrag (Zeigerlänge) und den Winkel φ an. Dann drehen wir uns am Ursprung des Koordinatensystems um den Winkel φ gegen den Uhrzeigersinn und laufen die Länge des Pfeils in diese Richtung. Diese Form der mathematischen Beschreibung bezeichnen wir als Exponentialform. Beide Formen beschreiben die gleiche komplexe Zahl, denn sie enden beide am gleichen Punkt in der komplexen Ebene.
Drehung und Länge
Wir trennen die Drehung in der komplexen Ebene um den Winkel φ von der Länge des Zeigers. Beide Effekte wollen wir unabhängig voneinander betrachten. Die Länge soll keine Drehung enthalten und die Drehung keine Länge. Eine reine Drehung ohne Längenänderung zu erhalten ist nicht trivial. Dafür brauchen wir einen Drehoperator mit der Länge 1. Die Länge entspricht mathematisch dem Betrag. Wir suchen also eine allgemeine mathematische Beschreibung eines Zeigers der Länge 1, der um den Winkel φ gedreht ist. In der Mathematik bezeichnen wir so einen Operator als „Einheitsvektor“.
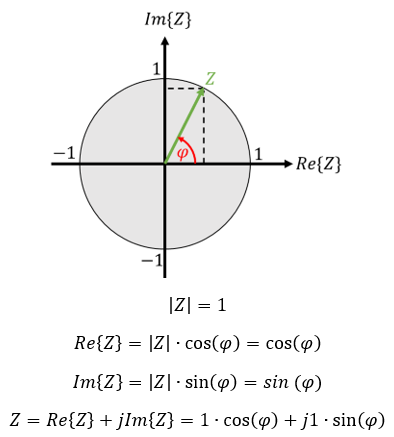
Wir betrachten einen Kreis in der komplexen Ebene mit Radius 1. Der Fußpunkt des Zeigers liegt immer im Ursprung des Koordinatensystems. Ein Zeiger, der vom Mittelpunkt des Kreises auf den Kreis zeigt, weist immer die Länge 1 auf. Die Spitze des Pfeils kann überall auf den Kreis zeigen. Damit ändert sich immer der Winkel φ, aber nie die Länge des Zeigers. Dieser Zeiger ist ein reiner Richtungsvektor in der Vektorrechnung. Auch ein Richtungsvektor hat immer die Länge 1.
Dieser Zeiger Z ist ein Drehoperator. Wenn wir Z mit einem konstanten Faktor multiplizieren, dann beschreibt der Faktor die Länge und Z die Richtung des Zeigers in der komplexen Ebene. Wir beschreiben eine reine Drehung um φ ohne Längenänderung als cos(φ) + j ∙ sin(φ).
Es gibt eine geniale Eigenschaft komplexer Zahlen in der komplexen Ebene, die eine extrem einfache mathematische Beschreibung einer Drehung um einen Winkel φ erlaubt. Es gilt (ohne Herleitung):

Wir drehen also einen Vektor um den Winkel φ, indem wir ihn mit ejφ multiplizieren. Die „reine“ Länge eines Vektors ohne Drehinformation bekommen wir aus dem Betrag des Vektors. Den haben wir weiter oben schon betrachtet. Es gilt am Beispiel der Zahl Z4 = 4 – j10:
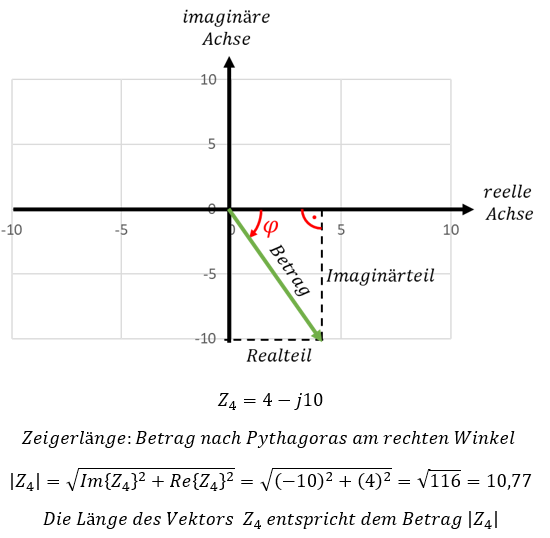
Wir können mit dem Winkel φ dem Betrag einer komplexen Zahl Realteil und Imaginärteil ausrechnen (und umgekehrt):


Sieh sehen, dass beide Darstellungsformen den gleichen Vektor beschreiben.
Wir können jetzt als Beispiel einen Vektor zeichnen, der die Länge 5 und die Richtung 45° aufweist. Wir zeichnen dafür einen Kreis mit Radius 5. Jeder Vektor, der vom Ursprung startet und auf diesem Kreis endet, weist die Länge 5 auf. Dann geben wir dem Vektor den Winkel 45° Wir starten in der Richtung 0° nach rechts. Dann drehen wir gegen den Uhrzeigersinn um 45°, wir lassen ihn also nach oben rechts zeigen.
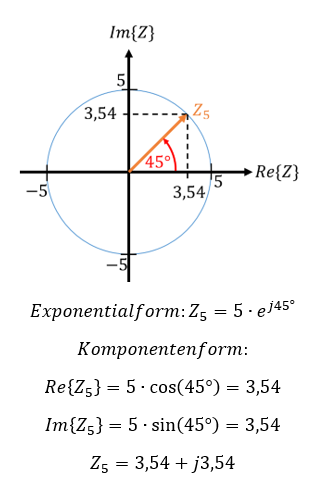
Sie sehen, dass Realteil und Imaginärteil immer kleiner (oder gleich) der Vektorlänge sind. Wir können den Vektor jetzt verlängern, indem wir ihn mit einem konstanten Wert multiplizieren. Wir verdoppeln seine Länge, indem wir ihn mit 2 Multiplizieren. Dadurch ändert sich seine Richtung nicht. Es gilt:
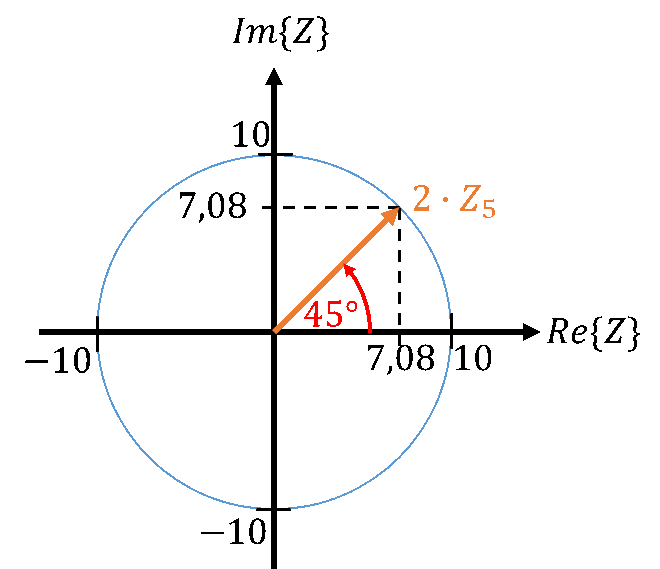
Wir können den Vektor Z5 auch drehen, ohne ihn zu verlängern. Um ihn um 90° zu drehen, multiplizieren wir ihn mit dem Drehoperator ej90°. Dieser Drehoperator hat die Länge 1, deshalb ändert sich durch die Multiplikation seine Länge nicht. Es gilt:
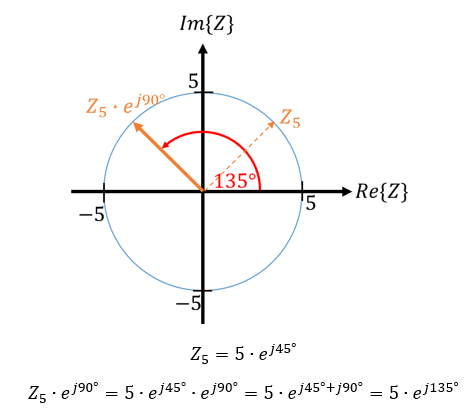
Durch die Drehung bleibt die Länge unverändert. Wenn Sie im Uhrzeigersinn drehen wollen, dann nehmen Sie eine negative Zahl im Exponenten des Drehoperators.
Sie sollten jetzt testen, ob Sie den Stoff verstanden haben, indem Sie folgende Aufgabe lösen:
Aufgabe
Gegeben ist der Vektor Z6 = 3 ∙ ej225°. Zeichnen Sie den Vektor in die komplexe Ebene ein und berechnen Sie Realteil und Imaginärteil des Vektors. Anschließend multiplizieren Sie den Vektor mit Z7 = 5 ∙ Z6 ∙ ej45°. Was passiert durch diese Multiplikation? Trennen Sie den Effekt auf in Längenänderung und Drehung.
Rechenoperationen
Wir können komplexe Zahlen in Komponentenform addieren und subtrahieren. Das geht in Exponentialform so ohne Weiteres nicht. Es gilt:
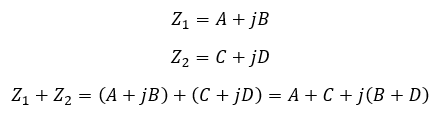
Addition und Subtraktion funktionieren vom Prinzip her gleich. Wir können sie auch multiplizieren und dividieren. Das sieht in Komponentenform folgendermaßen aus:
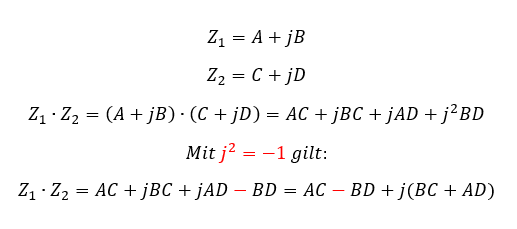
Die Lösung ist ziemlich hässlich. Es ist oft schöner, die Zahlen zunächst in Exponentialform umzuwandeln und dann zu multiplizieren. Dann gilt:
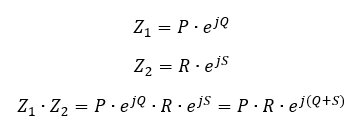
Die Division ist ähnlich. Es gilt (nur in Exponentialform):
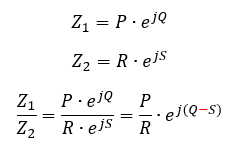
In der Elektrotechnik müssen wir zur Berechnung von Spannungen und Strömen Maschengleichungen, Knotengleichungen, Spannungsteiler und Stromteiler ausrechnen. Dafür brauchen wir die 4 Grundrechenarten. Für komplexe Spannungen und Ströme sollten Sie die passende Darstellungsform wählen. Addition und Subtraktion erfolgen in Komponentenform und Multiplikation und Division sind in Exponentialform am einfachsten.
Zum Glück beherrscht Ihr Taschenrechner alle Rechenarten in jeder Darstellungsform. Ich werde in diesem Tutorial und in den Lösungen zu den Übungsaufgaben immer die passende Darstellungsform für das Vorrechnen wählen.
Weiter