Ein Kondensator ist ein Speicher für elektrische Energie. Er speichert Energie in Form von getrennten Ladungen. Ein Stausee hält für das Wasserkraftwerk immer genügend Wasser vorrätig. Der Kondensator hält getrennte Ladungen vorrätig, die von dort aus in Form von Strom in eine Schaltung fließen können. Wenn ein Verbraucher kurzfristig viel Leistung benötigt, kann diese aus dem Kondensator entnommen werden.
Ein Kondensator verhält sich in einer Schaltung so ähnlich wie eine Quelle. Der Unterschied besteht darin, dass die Ladung, die entnommen worden ist, auch von der Schaltung wieder nachgefüllt werden muss. Der Kondensator kann in der Anwendung auch vollständig geleert werden. Er kann nur nicht weiter als bis zu seinem Maximum gefüllt werden.
Ein Kondensator besteht in der einfachsten Form aus zwei parallelen Metallplatten, die sich nicht berühren und zwischen denen sich elektrisch nichtleitendes Material (z. B. Luft) befindet. Wenn getrennte Ladung im Kondensator gespeichert ist, dann sind auf der einen Platte viele, und auf der anderen wenige positive Ladungen vorhanden (technische Stromrichtung). Jede der Platten ist mit einem Anschluss verbunden, mit dem der Kondensator mit den anderen Bauelementen der Schaltung verbunden wird. Zwischen den Platten kann eine Spannung gemessen werden, sobald Ladungen darauf getrennt sind.
Die Kapazität C eines Kondensators beschreibt seine Speicherkapazität für Ladungen. Sie gibt wie das Volumen des Eimers an, wie viel getrennte Ladung maximal im Kondensator gespeichert werden kann. Es gilt
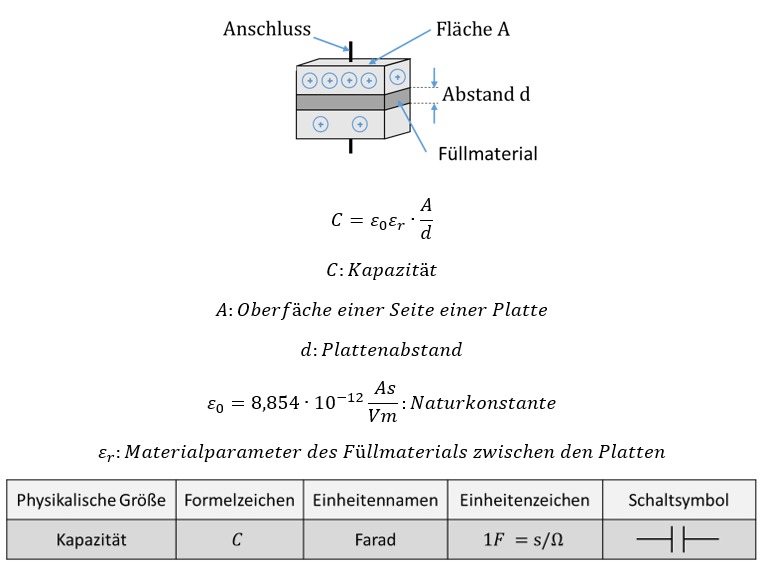
Die Kapazität C wird in der Einheit Farad angegeben. Die Kapazität wird von der Geometrie des Aufbaus und einem Materialparameter bestimmt. Steigt die Fläche, steigt auch die Kapazität, denn mehr Ladung findet an der Oberfläche der Platten Platz. Sinkt der Abstand d, steigt die Kapazität ebenfalls an.
Optimierung der Kapazität
Hinweis: Dieser Abschnitt bis zur nächsten Überschrift ist nicht prüfungsrelevant.
In einem Smartphone sind tausende Kondensatoren verbaut. Damit das Smartphone in die Hosentasche passt, müssen alle Bauelemente darin sehr kleine Abmessungen aufweisen. Dennoch werden Kondensatoren mit großer Kapazität benötigt, um z. B. kurzfristig Energie für das Versenden einer Nachricht bereitzustellen.
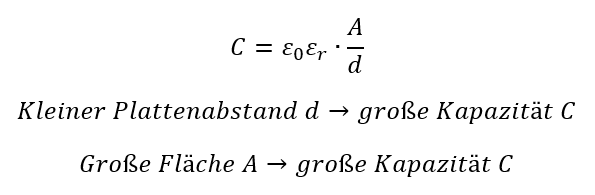
Wir brauchen also Kondensatoren mit großer Kapazität bei kleiner Fläche A. Dafür machen wir den Abstand d möglichst klein. Je kleiner der Abstand d zwischen den Platten ist, desto kleiner ist die maximale Spannung des Kondensators. Bringen wir getrennte Ladungen extrem nah zusammen und erhöhen die Spannung immer weiter. Dann „schlagen“ die Ladungen ab einer bestimmten Spannung durch den Isolator zwischen den Platten hindurch, obwohl der Isolator eigentlich Strom nicht leitet. Sie bilden einen leitfähigen Tunnel durch den Isolator. Der Kondensator ist danach defekt, die Schaltung meistens auch. Wir können den Plattenabstand d also nicht beliebig klein machen.
Wir verwenden in Kondensatoren Isolationsmaterial mit möglichst großem Materialparameter εr. Die maximale Spannung bei sehr kleinem Abstand d ist auch vom Isolationsmaterial abhängig. Wenn die Medien von Rohstoffen aus Krisengebieten berichten, die für die Herstellung von Smartphones benötigt werden, dann sprechen sie u. a. von diesem Füllmaterial der Kondensatoren. Ein technisch gut geeigneter Füllstoff mit hohem εr ist z. B. Tantal. Die Naturkonstante ε0 können wir nicht ändern.
Über den Aufbau der Kondensatoren können wir die Kapazität weiter optimieren. Dafür legen wir nicht nur 2 Platten übereinander, sondern sehr viele Platten. Zwischen den Platten befindet sich jeweils ein Isolator. Jede zweite Platte ist jeweils miteinander verbunden, so dass sich eine möglichst große Fläche A bildet.
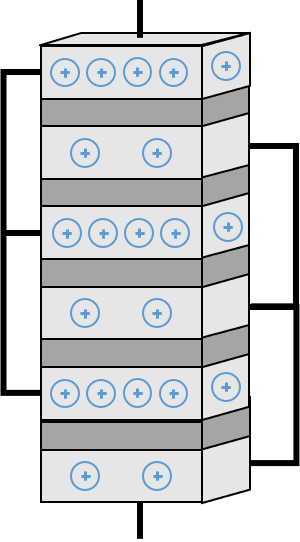
Die Kapazität C bestimmt den Zusammenhang zwischen Ladung Q und Spannung U nach folgender Formel:
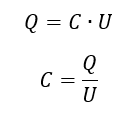
Es ist einfach, viel Ladung zu trennen, wenn dafür viel Spannung bereitsteht. Ein „guter“ Kondensator mit hoher Kapazität kann mit wenig Spannung viel Ladung getrennt halten. Dies ist insbesondere in batteriebetriebenen Systemen wichtig, die mit wenig Spannung auskommen müssen. Wird einem Kondensator Ladung Q entnommen, sinkt seine Spannung U. Sie sinkt umso weniger stark, je größer die Kapazität C ist.
Analogie zum Wassereimer
Hinweis: Dieser Abschnitt bis zur nächsten Überschrift ist nicht prüfungsrelevant.
Betrachten wir das Modell des Wassereimers aus dem letzten Kapitel. Es besteht eine Analogie zwischen Wassereimer und Kondensator.
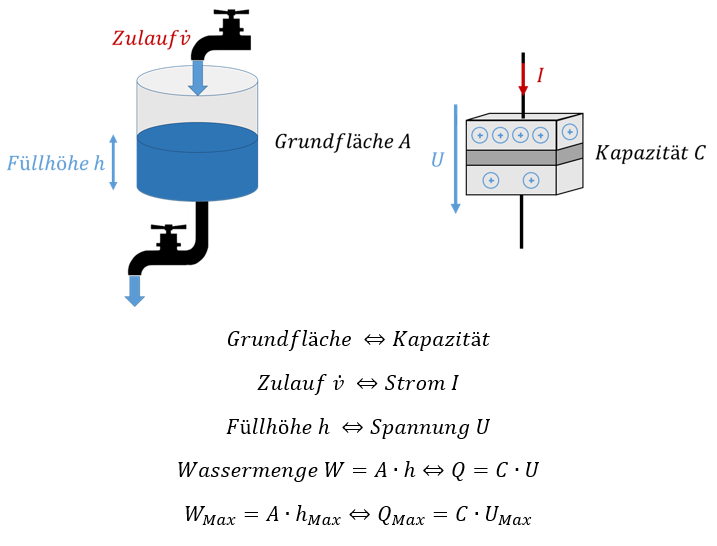
Am Eimer haben wir den Zu- bzw. Ablauf als Eingangsgröße definiert. Die Ausgangsgröße ist der Füllstand h. Beim Kondensator ist der elektrische Strom die Eingangsgröße. Sie beschreibt die Zulaufgeschwindigkeit der Ladung Q. Die Ausgangsgröße ist die Spannung U.
Die Kapazität C des Kondensators entspricht der Grundfläche A des Eimers. Der Füllstand h entspricht der Spannung U. Die Wassermenge im Eimer entspricht der Ladung Q, die im Kondensator getrennt ist.
Wird dem Eimer Wasser entnommen, sinkt der Füllstand h. Wird dem Kondensator getrennte Ladung Q entnommen, sinkt die Spannung U. Je größer die Grundfläche A des Eimers ist, desto weniger stark sinkt der Füllstand h, wenn Wasser abfließt. Je größer die Kapazität C des Kondensators ist, desto weniger stark sinkt die Spannung U, wenn getrennte Ladung abfließt. Die maximale Wassermenge ist durch das Eimervolumen V = A ∙ hMax begrenzt. Die maximale Ladungsmenge QMax ist durch die Kapazität C multipliziert mit der maximalen Spannung UMax begrenzt.
Mit dem Wasser aus dem Eimer, der als Wasserspeicher dient, soll jetzt ein Wasserrad angetrieben werden. Dafür bekommt er zunächst von oben einen Zulauf und unten einen Ablauf:
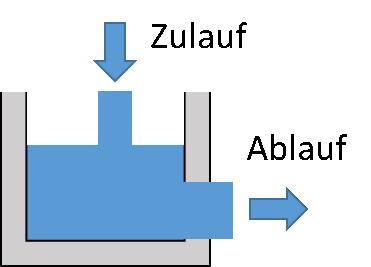
Es gibt einen Zufluss als Rohr, mit dem das Wasserrad angetrieben wird. Das Problem ist, dass das Wasserrad die meiste Zeit mehr Wasser bekommt als dort gebraucht wird. In kurzen Intervallen wird allerdings viel mehr Wasser benötigt, als der Zulauf zur Verfügung stellt.
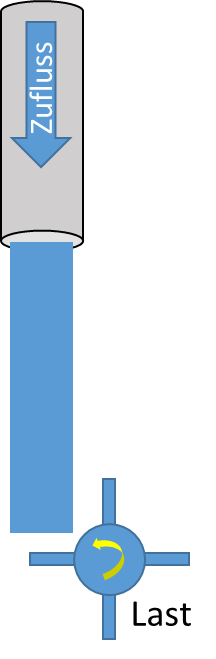
Als Lösung wird ein Teil des Wassers in den Speicher geleitet. Der Speicher kann bei Bedarf zusätzliches Wasser bereitstellen. Ein Ventil steuert den Ausgang des Speichers. Er wird mit dem überschüssigen Wasser gefüllt.
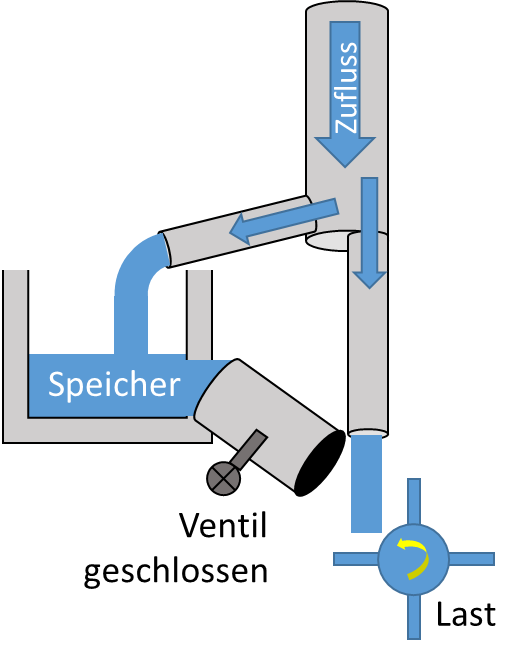
Jetzt kommt weniger Wasser kontinuierlich an der Last an. Das restliche Wasser wird im Speicher gespeichert. Der Füllstand des Speichers steigt kontinuierlich an, so lange das Ablaufventil geschlossen ist. Wird jetzt kurzzeitig von der Last mehr Wasser benötigt also die Zuleitung liefern kann, wird das Ablaufventil geöffnet.
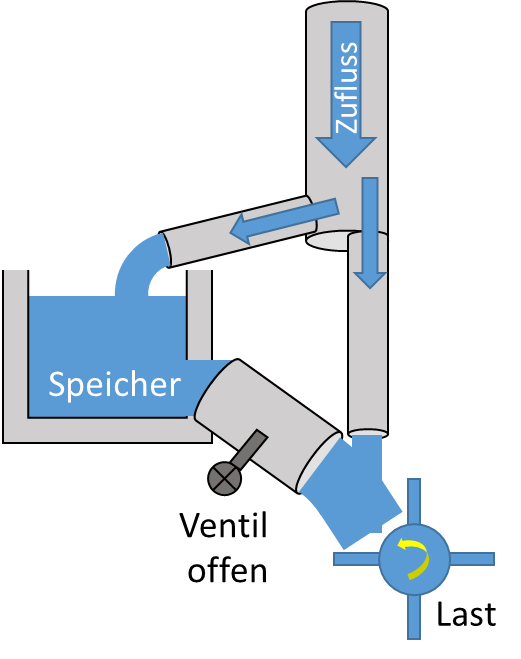
Der Füllstand des Speichers leert sich. Die Last bekommt kurzzeitig mehr Leistung.
Negative Spannung
Die Analogie ist begrenzt. Der Eimer kann nicht negativ gefüllt werden. Weniger als leer geht nicht. Ein Kondensator kann aber mit einer negativen Spannung aufgeladen werden. Dafür wird der Ladungsüberschuss statt auf der oberen Platte einfach auf der unteren Platte platziert.
Betrachten wir einen ungeladenen Kondensator. Beide Platten sind gleich geladen. Jetzt fließt ein positiver Strom in den oberen Anschluss des Kondensators hinein. Der Strom fließt immer im Kreis. Strom geht in einem Bauelement nicht verloren, er fließt also unten aus dem Kondensator wieder heraus. So wird die obere Platte geladen und die untere entladen. Damit ist die Spannung am Kondensator positiv. Diesen Fall zeigt die obere der folgenden drei Abbildungen.
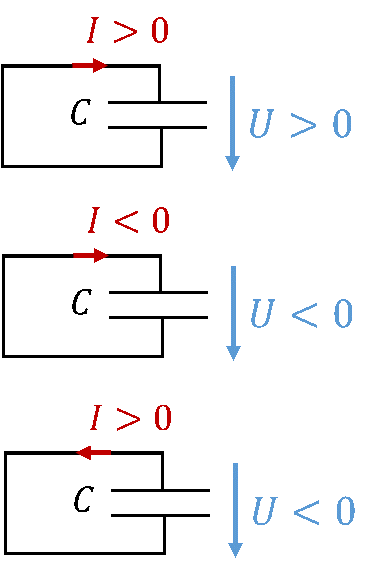
Betrachten wir erneut einen ungeladenen Kondensator. Beide Platten sind gleich geladen. Jetzt fließt ein negativer Strom in den oberen Anschluss des Kondensators hinein. Er fließt unten aus dem Kondensator wieder heraus. So wird die obere Platte entladen und die untere geladen. Damit ist die Spannung am Kondensator negativ. Das zeigt die mittlere Abbildung.
Einen negativen Strom können Sie sich als positiven Strom in die andere Richtung vorstellen. Drehen Sie also den Strompfeil der mittleren herum und nehmen Sie positiven Strom. Diesen Fall zeigt die untere Abbildung. Sie dient nur der Veranschaulichung einer negativen Stromrichtung, sie zeigt keinen neuen Zusammenhang.
Zusammenhang zwischen Spannung und Strom
In Kapitel Rechnen mit Speichern ist gezeigt worden, dass der Füllstand eines Eimers vom Integral des Zu- bzw. Ablaufs bestimmt wird. Es gilt an Eimer und Kondensator:
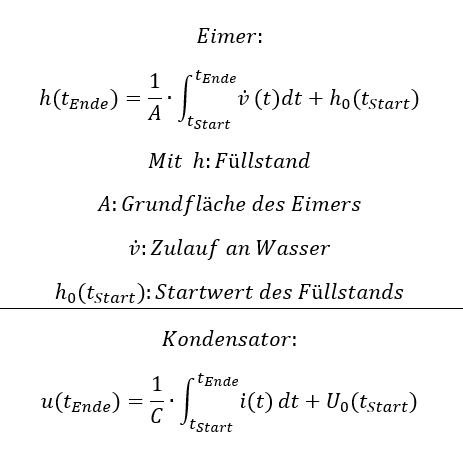
Fließt ein Strom in den Kondensator hinein, steigt die Spannung an. Mit Hilfe eines Stroms wird also am Kondensator zusätzliche Ladung getrennt, die Energie im Kondensator steigt an. Fließt ein Strom aus dem Kondensator heraus, sinken seine Spannung und seine Energie. Da der Stromfluss die Ursache für die Spannung am Kondensator ist, verwende ich für die erste elektrische Betrachtung eine Stromquelle, die mit dem Strom IC die Spannung am Kondensator UC verändert. Betrachten wir ein Zahlenbeispiel:
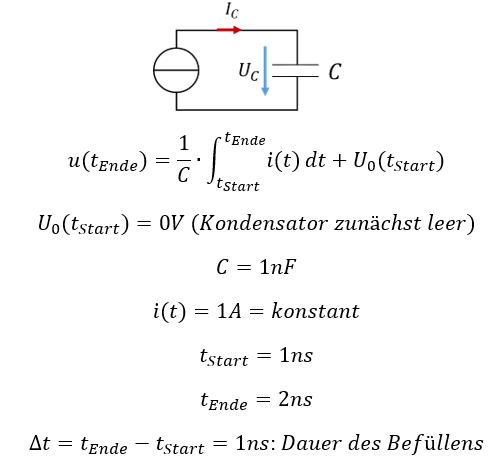
Zunächst stellen wir fest, dass der Strom während des Ladevorgangs über der Zeit konstant ist. Das vereinfacht die Rechnung. Die folgende Vereinfachung gilt nur für über der Zeit konstante Ströme. Ändert sich der Strom über der Integrationszeit, müssen Sie die Stammfunktion für das Integral bilden. Bei konstantem Strom gilt:
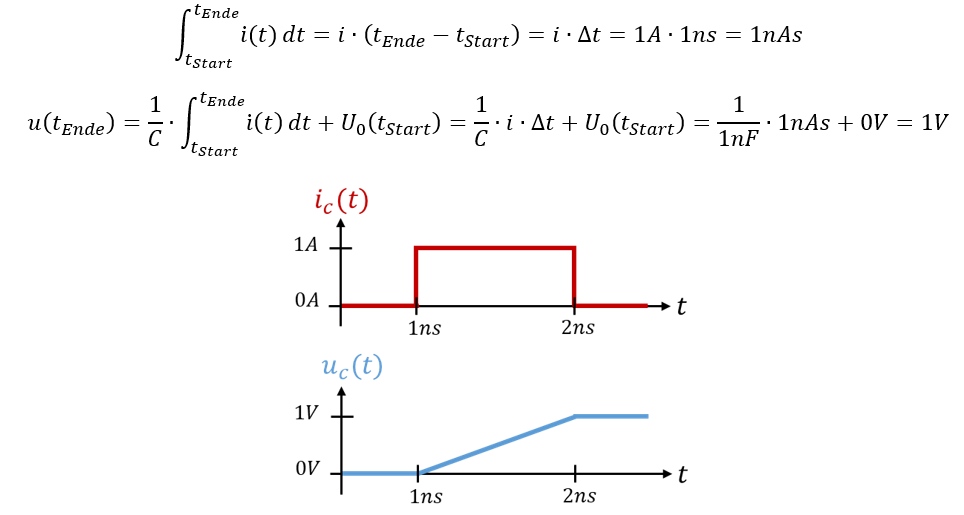
Die Spannung am Kondensator beträgt nach der Befüllung UC = 1V. Wenn wieder Strom in den Kondensator hinein oder aus ihm hinaus fließt, ändert sich die Spannung erneut. Lassen wir also anschließend für Δt = 1ms den Strom i = -1µA aus dem Kondensator hinaus fließen. Der Richtungswechsel im Strom führt mathematisch zu einem Vorzeichenwechsel in der Formel. Weil der Strom erneut während der Integrationszeig konstant ist gilt:
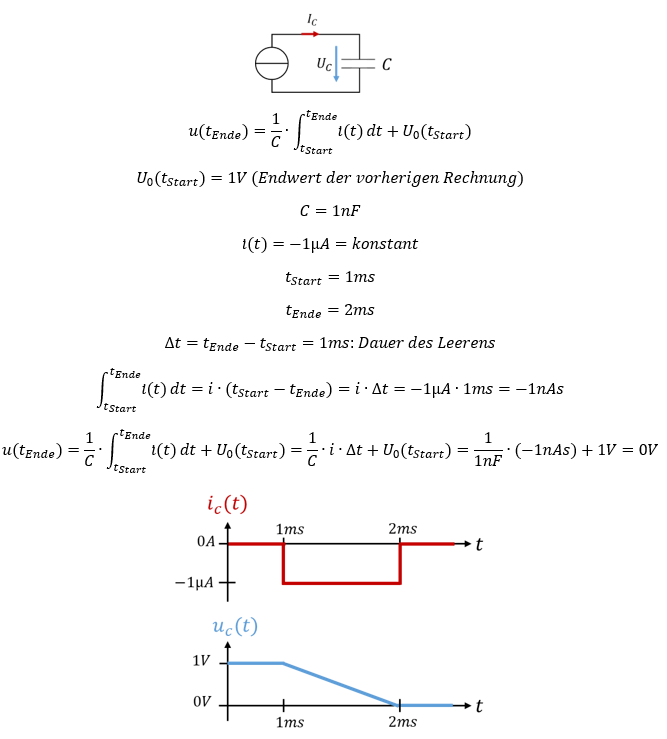
Die Umkehrfunktion des Integrals ist die Ableitung. Ist die Spannung am Kondensator gegeben und der Strom gesucht, wird die Spannungsgleichung durch Ableitung auf beiden Seiten folgendermaßen umgeformt:
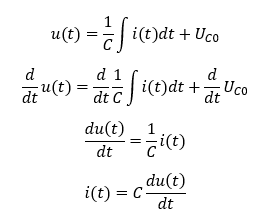
Leistung und Energie
Betrachten wir für die Leistung zunächst das Wassermodell: Die mechanische Leistung, die vom Speicher durch das Wasser an die Last abgegeben wird, ist proportional zur Wassermenge multipliziert mit der Höhe, von der das Wasser aus auf das Schaufelrad fällt. Je geringer der Füllstand des Speichers ist, desto weniger Leistung kann er abgeben, denn das Wasser kommt dann mit weniger Druck an der Last an. Ein guter Speicher verfügt deshalb über eine so große Grundfläche, dass sich während des Ablassens die Füllhöhe nur wenig ändert.
Die Leistung ist als Produkt aus Spannung und Strom definiert. Am Kondensator liegt Leistung vor, wenn sowohl Spannung als auch Strom zeitgleich vorhanden sind. Das ist nur während eines Ladevorgangs und während eines Entladevorgangs der Fall.
Betrachten wir als nächstes die Energie, die ein Kondensator speichern kann. Es gilt
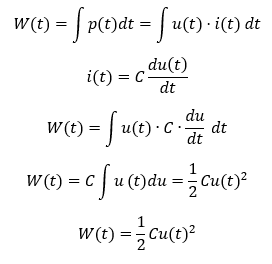
Die im Kondensator gespeicherte Energie hängt also quadratisch von der Spannung U und linear von der Kapazität C ab. Je mehr Spannung an einem Kondensator anliegt, desto mehr Energie ist in ihm gespeichert.