Kondensator und Widerstand

Zur Vereinfachung betrachten wir den Fall, dass zwischen einer idealen Spannungsquelle und einem Kondensator nur ein Widerstand liegt. Betrachten wir die Maschengleichung und die Bauelementgleichungen der Schaltung. Es gilt

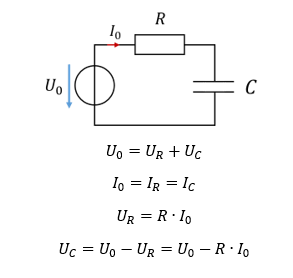
Betrachten wir zunächst den leeren Kondensator mit U_C = 0V. Die Spannung am Widerstand entspricht dann der Spannung der Quelle. Es gibt keinen Arbeitspunkt, bei dem mehr Spannung am Widerstand abfällt. Deshalb ist der Strom bei leerem Kondensator maximal groß.

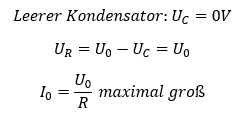
Der Strom lädt den Kondensator auf. Es fließt so lange Strom in den Kondensator, bis er auf die Quellenspannung aufgeladen ist. Mehr Spannung kann am Kondensator nicht anliegen. Betrachten wir als nächstes einen maximal aufgeladenen Kondensator:

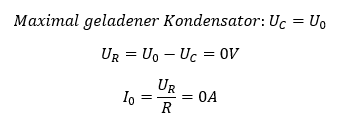
In diesem Arbeitspunkt fließt kein Strom. Die Potentiale links und rechts vom Widerstand sind gleich groß. Über dem Widerstand fällt keine Spannung mehr ab, also ist der Strom durch den Widerstand 0. Die Spannung am Widerstand hängt davon ab, wie viel Spannung am Kondensator abfällt, also wie stark er bereits geladen ist. Je höher die Kondensatorspannung ist, desto kleiner wird der Strom.

Mit dieser Erkenntnis wechseln wir ins Wassermodell für eine anschauliche Erklärung.

Wassermodell

Hinweis: Dieser Abschnitt bis zur nächsten Überschrift ist zwar nicht prüfungsrelevant, er hilft aber sehr beim Verständnis.

Wir betrachten einen sehr großen, flachen See in fester Höhe, der eine ideale Spannungsquelle für Wasser darstellt. Dieser See behält seine Höhe und seinen Füllstand unabhängig davon, wie viel Wasser entnommen wird. Aus diesem See wird ein Wasserspeicher (Eimer) über ein Rohr gefüllt. Dies entspricht dem elektrischen Schaltbild.

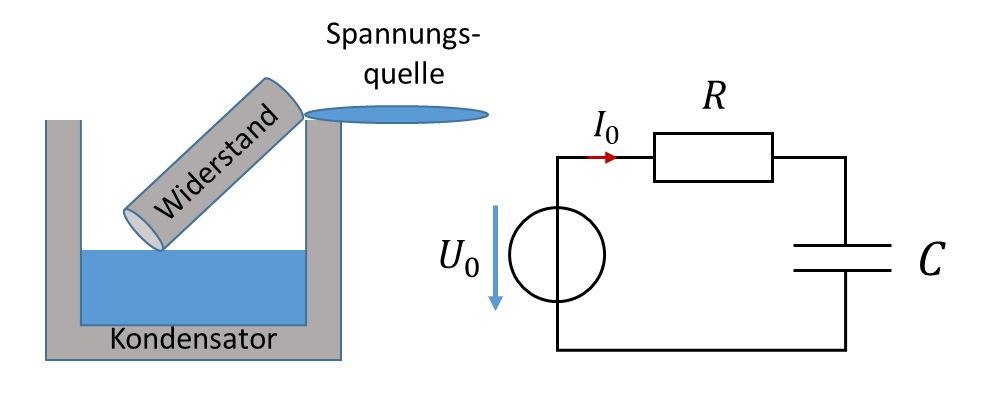
Die Spannung der Quelle entspricht der Höhe des Sees. Sie ist unveränderlich. Die Spannung des Kondensators entspricht der Füllhöhe des Speichers. Die Spannung am Widerstand entspricht der Steigung des Rohrs, also dem Höhenunterschied zwischen den Rohrenden.

In der Reihenschaltung aus R und C teilt sich die Quellenspannung auf den Widerstand und den Kondensator auf. Die Höhe des Sees muss sich in der Analogie also auf die Füllhöhe des Speichers und die Steigung des Rohrs aufteilen. Deshalb schwimmt das untere Ende des Rohrs auf dem Wasser im Speicher. Die Steigung des Rohrs wird damit kleiner, wenn der Speicher höher gefüllt ist.

Ist der Speicher leer, ist die Steigung des Rohrs maximal. Es fließt also maximal viel Wasser in den Speicher. Ist der Speicher voll, ist keine Steigung mehr für das Rohr übrig. Es fließt kein Wasser mehr in den Speicher. Je voller der Speicher ist, desto geringer ist der Zulauf durch das Rohr, weil dessen Steigung sinkt. So läuft das Aufladen eines Kondensators über einen Widerstand anschaulich ab.

Die folgende Abbildung zeigt Zahlenwerte zu den elektrischen Größen und Grafiken zu den jeweiligen Füllständen des Kondensators im Wassermodell:

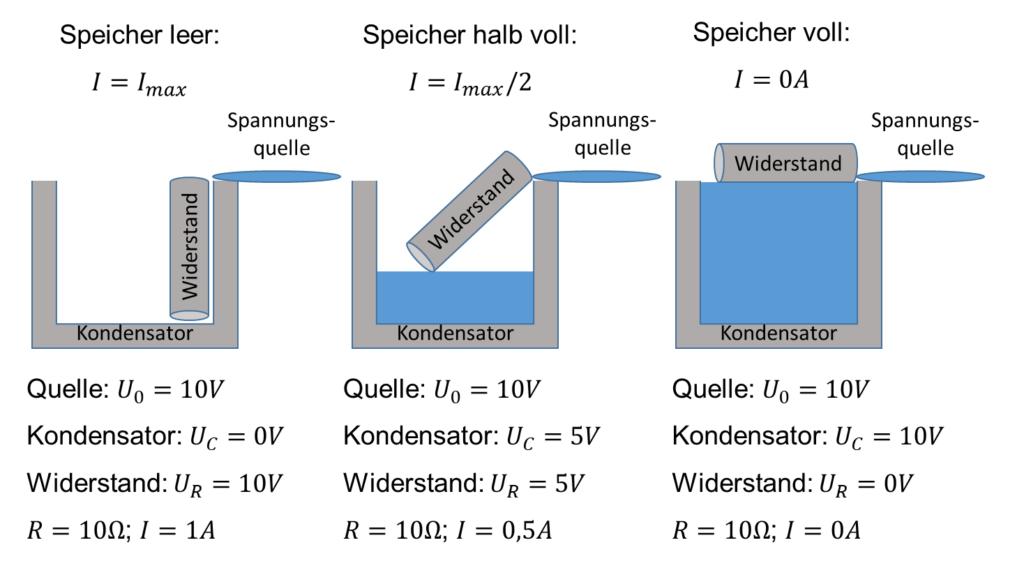
Der Eimer ist im linken Bild leer. Das Rohr die maximale Steigung auf und es fließt maximal viel Wasser in den Eimer. Dies entspricht einem Widerstand, dessen Spannung bei leerem Kondensator maximal groß ist, und durch den deshalb maximal viel Strom in den Kondensator fließt.

Je voller der Eimer wird, desto geringer wird die Steigung des Rohrs, also fließt immer weniger Wasser in den Eimer hinein (mittleres Bild). Erreicht der Füllstand des Eimers die Höhe der Quelle, beträgt die Steigung des Rohrs 0, also fließt kein Wasser mehr in den Eimer hinein. Das zeigt das rechte Bild.

Zeitverläufe

Der Zeitverlauf eines Füll-Vorgangs sieht etwa so aus:

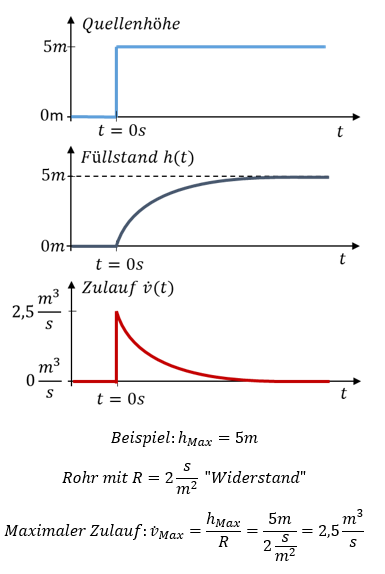
Wir brauchen für die Berechnung des Ladevorgangs einen Schalter. Wäre der Speicher dauerhaft mit der Quelle verbunden, dann wäre er einfach immer aufgeladen. Das ist langweilig. Die Quelle wird stattdessen durch das Schließen eines Schalters (beim Wasser: Ventil) zum Zeitpunkt t = 1s mit dem leeren Speicher verbunden. In der Elektrotechnik wird eine Spannungsquelle über einen Schalter mit der Reihenschaltung aus Widerstand und Kondensator verbunden.

Mathematische Betrachtung

Die mathematische Betrachtung in diesem Abschnitt bis zur nächsten Überschrift ist für die Klausur nicht relevant. Die Lösung des Problems beschreibt eine Differenzialgleichung. Ihnen fehlt dafür wahrscheinlich die mathematische Grundlage. Also versuchen Sie einfach, die Berechnung halbwegs nachzuvollziehen.

Ab jetzt verwende ich in den Berechnungen Kleinbuchstaben für Spannung und Strom. Wir verwenden Großbuchstaben für konstante, über der Zeit unveränderliche Werte. Beim Laden und Entladen des Kondensators ändern sich Spannung und Strom über der Zeit, deshalb verwende ich Kleinbuchstaben. Nur die konstante Quellenspannung und die konstante Startspannung des Kondensators können weiter als Großbuchstaben geschrieben werden.

In der Reihenschaltung aus Widerstand und Kondensator gelten die Gleichungen:

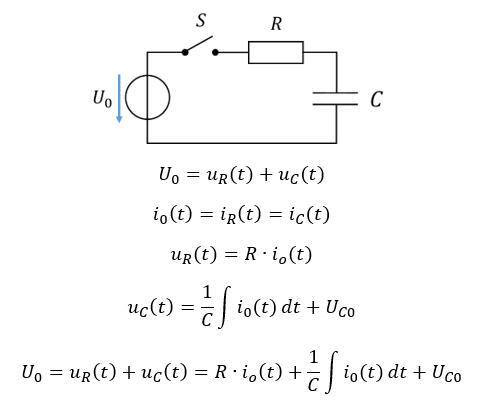
In der unteren Gleichung tauchen der Strom und dessen Ableitung in einer Gleichung auf. Diese Art von Gleichung wird als Differenzialgleichung bezeichnet. Die Lösung leite ich nicht her, ich gebe einfach das Ergebnis an. Anschließend plausibilisieren wir das Ergebnis, indem wir es in die Gleichung einsetzen. Es gilt für den Strom:

Weil in der letzten Zeile die Gleichung mit U₀ = U₀ erfüllt ist, haben wir offenbar etwas Richtiges für i₀ eingesetzt. Sonst wäre die Gleichung nach dem Einsetzen links und rechts nicht gleich. Damit ist gezeigt, dass die obere Gleichung für den Strom stimmt. Für die Spannung am leeren Kondensator mit U_C0 = 0V gilt dann:

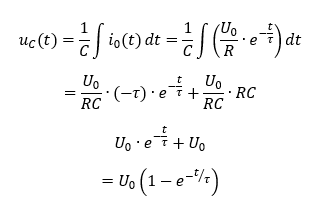
Die Verläufe von Spannung und Strom am Kondensator entsprechen denen am Speicher des Wassermodells. Um das Zuschalten der Quelle über Schalter S besser modellieren zu können, führe ich einen innere Spannung u_i ein. Bei offenem Schalter gilt u_i = 0V. Bei geschlossenem Schalter gilt u_i = U₀. Der Schalter wird bei t = 0s geschlossen.

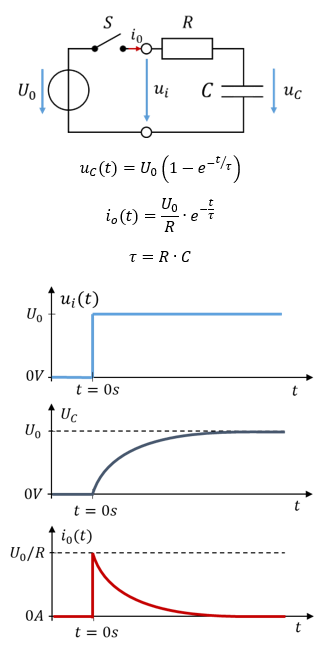
Betrachten wir die elektrischen Größen beim Schaltzeitpunkt und nach unendlich langer Zeit. Dafür setzen wir für die Zeit t die Werte 0s und ∞ ein. Es gilt:

Entladen eines Kondensators

Bisher haben wir den Kondensator nur aufgeladen. Ein Kondensator wird üblicherweise in eine Last entladen. Diese Last zeigt oft ein Verhalten wie ein Ohm´scher Widerstand. Deshalb wird hier nur der Fall untersucht, wie sich ein Kondensator über einen Widerstand entlädt. Dabei werden wieder Annahmen zur Vereinfachung gemacht:

Der Kondensator ist zu Beginn des Entladevorgangs mit einer Spannung U_C = U₀ aufgeladen. Er ist über einen Schalter zunächst von der Last entkoppelt und hält deshalb seine Spannung aufrecht.

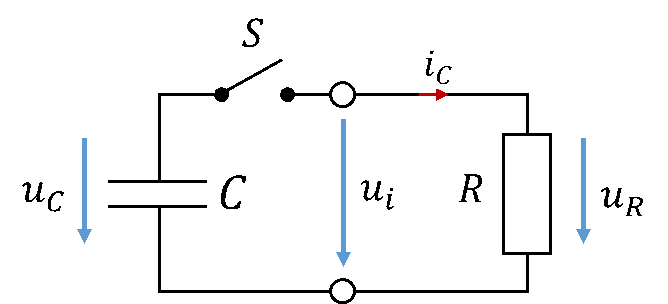
Jetzt schließen wir den Schalter und betrachten Spannung und Strom beim Entladen des Kondensators. Ich habe wieder die Hilfsgröße u_i hinter dem Schalter eingezeichnet.

Bei offenem Schalter gilt u_i = 0V. Bei geschlossenem Schalter S sind Kondensator und Widerstand parallelgeschaltet. Es gilt dann u_i = u_R. Die Gleichungen für Strom und Spannung für das Entladen lauten (wieder ohne Herleitung):

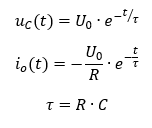
Betrachten wir wieder die einfachen Zeitpunkte t = 0s und t → ∞ zur Plausibilisierung der Gleichungen. Sobald der Schalter S geschlossen wird, liegt die Kondensatorspannung am Widerstand an. Die Spannung am Widerstand ist niemals größer als jetzt. Deshalb fließt der maximale Strom aus dem Kondensator heraus. Nach unendlich langer Zeit ist der Kondensator vollständig entladen. Dann ist auch am Widerstand keine Spannung mehr vorhanden. Der Strom beträgt dann also 0A.

Die Bedeutung von Tau(τ)

Tau hat die Einheit Sekunde, es ist also eine Zeitgröße. Sie beschreibt, wie langsam oder schnell ein Ladevorgang abläuft. Je größer Tau ist, desto mehr Zeit vergeht bis zum vollständigen Laden, also desto langsamer verläuft der Vorgang. Die Kurvenform des Ladens ändert sich mit Tau nicht.

Es gilt τ = RC. Je größer die Kapazität C des Kondensators ist, desto langsamer ist der Ladevorgang. Nach Q = C ∙ U müssen mehr Ladungen getrennt werden, bis der Kondensator seine Zielspannung erreicht. Ein größerer Widerstand reduziert den Ladestrom, deshalb dauert das Laden länger.

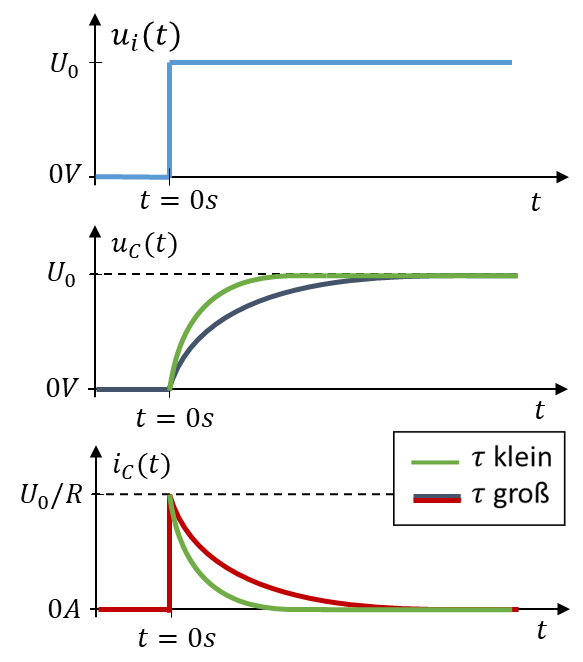
Die Kondensatorspannung erreicht zum Zeitpunkt t = τ den Wert 63% ihres Endwerts. Beim Aufladen gilt bei t = τ also u_C( τ)=0,63 ∙ U₀. Den Wert von τ kann man im Zeitverlauf ablesen. Es ist die Zeitdifferenz zwischen dem Zeitpunkt des Umlegens des Schalters und dem Zeitpunkt, bei dem die Kondensatorspannung 63% Ihres Endwerts erreicht hat.

Betrachten wir nochmal den Eimer. Einen Eimer mit größerer Grundfläche A umzuladen dauert länger. Die Fläche A ist analog zur Kapazität C. Ihn über ein schmaleres Rohr umzuladen dauert ebenfalls länger als über ein breites Rohr. Ein kleiner Rohrdurchmesser ist analog zu einem großen Widerstand. Also ist es plausibel, dass τ mit größerem R und größerem C auch größer wird.

Weiter