Magnetische Felder können geführt werden. Das läuft ähnlich ab wie beim elektrischen Strom. Angenommen wir trennen Ladung in einer Batterie, an die nichts angeschlossen ist. Die getrennte Ladung strebt den Ladungsausgleich an. Aber erst wenn ein elektrisch leitfähiger Weg für den Ladungsausgleich geschaffen ist, fließt Strom. Der Strom fließt entlang des leitfähigen Wegs, er wird also geführt. Das ist z. B. ein Kabel, das von der Batterie zum Verbraucher führt. Es fließt kein Strom neben dem Kabel her, weil Luft so eine geringe Leitfähigkeit für Strom hat.
Das magnetische Feld „fließt“ auch durch Luft. Die magnetische Leitfähigkeit von Luft ist zwar gering, aber viel höher als die elektrische Leitfähigkeit von Luft. Das ist in der Analogie so, als ob Strom auch durch Luft fließen würde. Dann würde an jeder Steckdose ein kleiner Strom zwischen den elektrischen Anschlüssen fließen.
Wenn Strom durch einen Leiter fließt, der von Luft umgeben ist, bildet sich also ein kleines Magnetfeld aus. Es gibt Material, das stark magnetisch leitfähig ist. Wird der Leiter von magnetisch gut leitendem Material umgeben, ist das Feld im Leiter viel stärker. Wir legen in Gedanken um einen Leiter herum magnetisierbares Material mit hoher magnetischer Leitfähigkeit in Form eines Ringkerns (blauer Ring in der Abbildung unten).
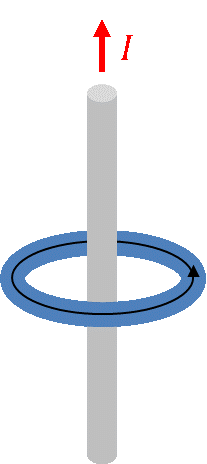
Das Magnetfeld „fließt“ dann nahezu vollständig durch den Kern. Nur ein sehr kleiner Teil, den wir in der Praxis vernachlässigen, existiert parallel in der Luft. Diesen Effekt nennt man „Feldbündelung“ oder „Feldführung“. Es wird erreicht, dass das Feld nicht mehr frei im Raum, sondern nur noch in einem vorgegebenen Bereich existiert. Der Anteil des geführten Felds am Gesamtfeld ist umso größer, je größer die magnetische Leitfähigkeit des Materials ist.
Ausrichtung des Felds
Bisher haben wir nur Leiter betrachtet, die eine gerade Linie bilden. Das Feld, das den Leiter umgibt, ist kreisförmig. Das ist für als Kraftrichtung oft nicht hilfreich. Es wäre besser, wenn das Feld in eine Richtung ausgerichtet wäre. Deshalb ändern wir im nächsten Schritt die Ausrichtung des Leiters. Wenn der stromdurchflossene Leiter kreisförmig angeordnet ist, dann bildet sich folgendes Feld aus:
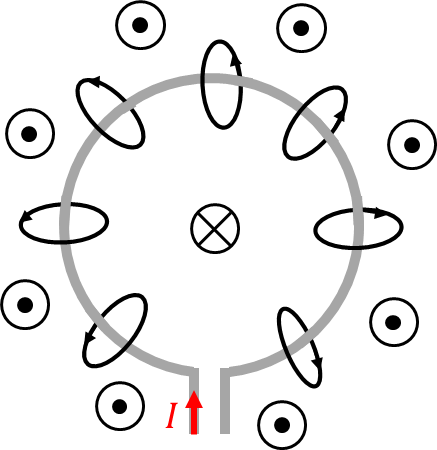
Die Leiterschleife ist in grau dargestellt. Darin fließt der Strom I. Es stellt sich ein Feld ein, das ringförmig um den Leiter herum verläuft. Das Feld hat die Form eines Donuts. Die Richtung der Feldlinien ermitteln Sie mit der Rechte-Hand-Regel.
Es ist zur Vereinfachung jeweils nur eine Feldlinie pro Position auf der Leiterschleife dargestellt. Natürlich sind auch weiter im Raum und näher am Leiter weitere Feldlinien vorhanden. Insgesamt verläuft das Feld in der Mitte der Leiterschleife in die Betrachtungsebene hinein. Außerhalb der Leiterschleife kommt es aus der Betrachtungsebene heraus. Für diese Richtungen werden wieder folgende Symbole verwendet:

Mit einer Leiterschleife schaffen wir es, dass das Feld innen in die eine Richtung und außen in eine andere Richtung verläuft. Wenn wir jetzt mehrere Leiterschleifen hintereinander setzen ergibt sich folgendes Feld:
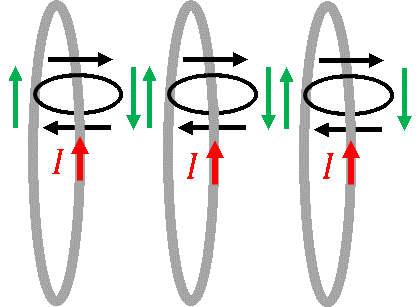
Es ist nur eine exemplarische Feldlinie pro Leiterschleife dargestellt. Die Feldlinien im innerhalb und außerhalb der Leiterschleifen (schwarze Pfeile) weisen innen alle nach rechts. Außen weisen sie alle nach links. Die in grün dargestellten Feldlinien zwischen den Leiterschleifen verlaufen jeweils gegenläufig. Da magnetische Felder genauso wie elektrische Felder dem Prinzip der Überlagerung unterliegen, werden Felder unterschiedlicher Quellen addiert. Die in grün dargestellten Feldanteile werden durch die Addition ausgelöscht, weil die die gleiche Intensität und unterschiedliches Vorzeichen (Richtung) aufweisen. Es bleibt also nur ein inneres und ein äußeres Feld:
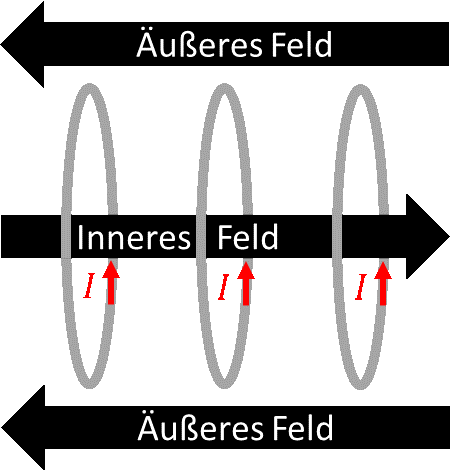
Wir wollen für mehrere Leiterschleifen nicht jedes Mal neu Strom bereitstellen. Deshalb schalten wir die Schleifen elektrisch in Reihe. Wir erhalten eine Spule:
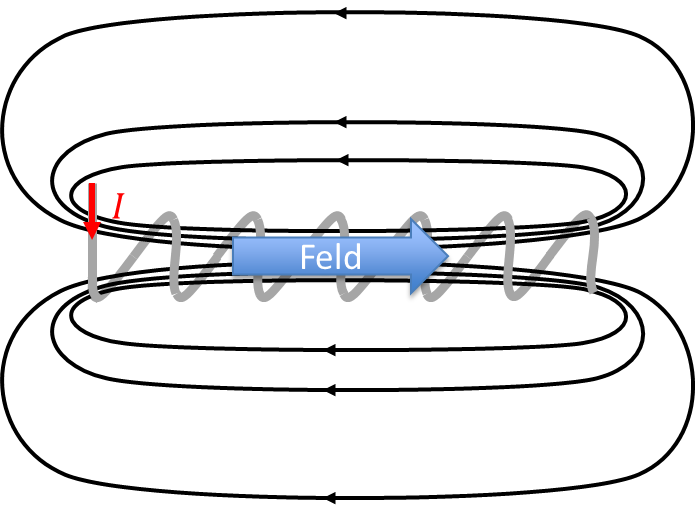
Wenn die Schleifen hinreichend eng zusammen liegen, dann erhalten wir in der Mitte ein magnetisches Feld, das nach rechts weist. Im Außenbereich weist das Feld nach links. Die Feldlinien sind geschlossen. Sie bilden Ovale. Im Innenbereich ist das Feld geführt. Die Feldlinien weisen innen alle in eine Richtung. Sie verlaufen nahezu parallel und sind nahezu homogen (konstante Feldliniendichte). Das Feld im Innenbereich einer Spule kann man also technisch gut nutzen.
Wenn wir aus dem Leiter N Leiterschleifen wickeln, durch die der gleiche Strom I fließt, dann wirkt der Strom N-fach. Die magnetische Feldstärke wird dann N-mal größer als bei einer Wicklung. Wir können also für das gleiche Feld entweder viel Strom und wenig Wicklungen oder wenig Strom und viele Wicklungen nutze. Das ist sehr vorteilhaft, denn damit bekommen wir einen weiteren Parameter an die Hand, mit der der notwendige Strom für die geforderte Feldintensität reduziert werden kann.
Im nächsten Schritt kombinieren wir die Feldführung durch Material mit der gerichteten Felderzeugung der Spule. Die Spule wird auf einen magnetisch leitfähigen Block mit sehr hoher magnetischer Leitfähigkeit gewickelt. Nahezu alle Feldlinien verlaufen dann durch den Block. Wichtig ist dabei, dass Feldlinien immer geschlossen sind. Der Block sollte also ebenfalls geschlossen sein.
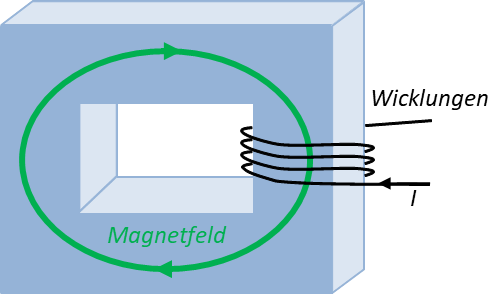
In der oberen Abbildung sind Feldlinien als Beispiel dargestellt. Die Richtung der Feldlinien ermitteln Sie mit der „Rechte-Hand-Regel“: Der Daumen zeigt in Richtung des Stroms. Dann weisen die gekrümmten Finger der rechten Hand in Richtung des Felds. Das Feld verläuft also im Uhrzeigersinn.
Wir haben mit der Feldführung und der Nutzung einer Spule folgendes erreicht:
– Das Feld verläuft nur innerhalb eines Blocks, nicht mehr frei in Luft. Damit kann das Feld direkt dahin geführt werden, wo es wirken soll. Es wird kein Feld mehr im Raum verschwendet.
– Der Block weist eine hohe magnetische Leitfähigkeit auf. Damit ist der magnetische Fluss bei gleichem Strom viel größer, als wenn wir in Luft arbeiten würden.
– N Windungen des Leiters führen alle den gleichen Strom. Das Feld jedes Leiters wird zu einem Gesamtfeld addiert (Überlagerung). Das Feld wird dadurch N Mal größer.
Weiter