Ein Hochpassfilter lässt Signale hoher Frequenz passieren und es dämpft Signale mit niedriger Frequenz. Betrachten wir als Beispiel eine typisch niederfrequente Störung: Das Netzbrummen bei fNetz = 50Hz. Alle Messsysteme, die am 230V-Netz angeschlossen sind, haben ein Störsignal mit kleiner Amplitude bei 50Hz im Messsignal. Nehmen wir für das Beispiel an, dass ein Nutzsignal die Frequenz ωNutz=100k 1/s aufweist. Die Kreisfrequenz der Störung beträgt ωStör=2πfNetz = 314 1/s. Spitzenwerte und Frequenzen sind im unteren Bode-Diagramm abgebildet.
Der Spitzenwert des Störsignals soll durch ein Filter möglichst stark reduziert werden, das Nutzsignal soll durch das Filter nicht beeinflusst werden. Die beiden Signale sind wieder im Frequenzbereich durch Pfeile dargestellt.
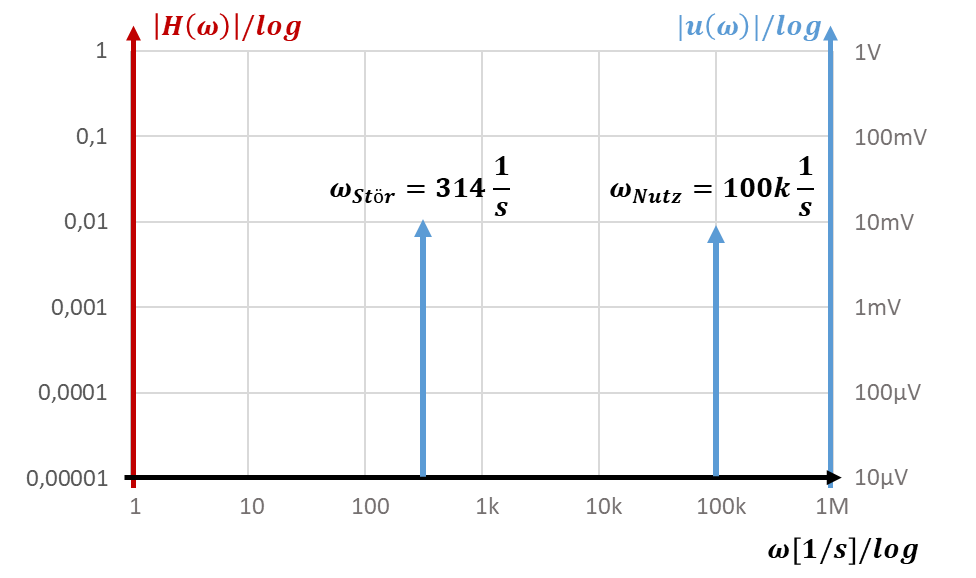
Ein passendes Filter lässt das Nutzsignal unverändert, indem es am Nutzsignal einen waagerechten Verlauf mit |H|=1 aufweist. Die nächste Eckfrequenz liegt um Faktor 10 vom Nutzsignal entfernt, sonst hat das Filter bereits einen zu hohen Einfluss auf das Nutzsignal (siehe die Diskussion dazu im Kapitel Tiefpass). Es dämpft das Störsignal, der Betrag seiner Übertragungsfunktion ist bei ωStör kleiner als 1. Dies wird durch folgendes Wunsch-Bode-Diagramm eines Filters beschrieben:
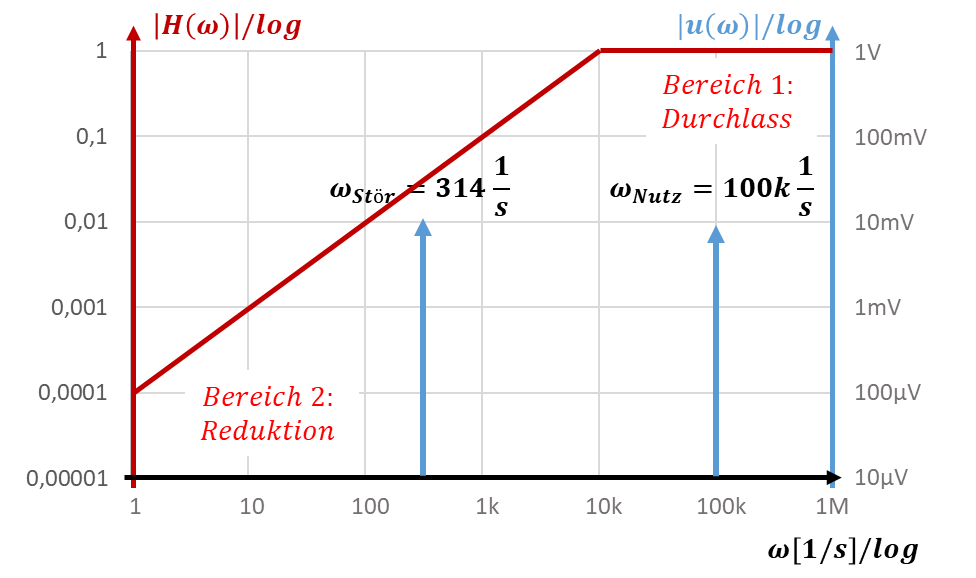
Aus dem Diagramm lesen wir ab, dass das Störsignal durch das Filter etwa um Faktor 0,03 verstärkt wird. Es wird also ungefähr um Faktor 30 gedämpft. Das Verhalten wird „Hochpass“ genannt, denn es lässt Signale hoher Frequenzen passieren und dämpft Signale niedriger Frequenzen.
Realisierung und Dimensionierung
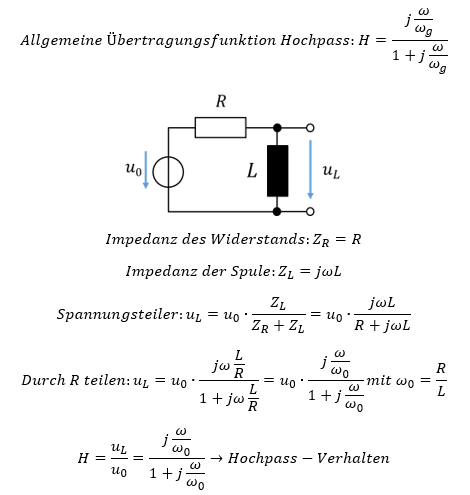
Zunächst wird eine passive Realisierung ohne Operationsverstärker diskutiert. Die Lösung nutzt erneut aus Kostengründen statt einer Spule einen Kondensator. Das einfachste Hochpass-Filter wird durch die Reihenschaltung aus Kondensator und Widerstand aufgebaut:
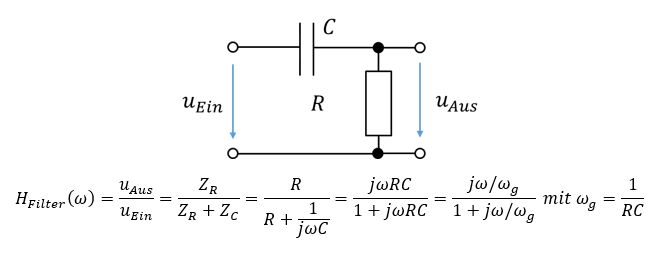
Im letzten Umrechnungsschritt habe ich den Bruch mit jωC erweitert. Betrachten wir zunächst wieder die beiden Bereiche der Übertragungsfunktion:

Das Verhalten des Bode-Diagramms passt zur Übertragungsfunktion der Schaltung. Also realisiert diese Schaltung (passives) Hochpass-Verhalten.
Phasenverlauf
Die Hochpass-Übertragungsfunktion beinhaltet das „j“ der komplexen Zahlen. Dadurch ändert sich die Phase des Signals zwischen Eingang und Ausgang der Schaltung. Betrachten wir nur die Phasendrehung unabhängig vom Betrag der Übertragungsfunktion. Es gilt:
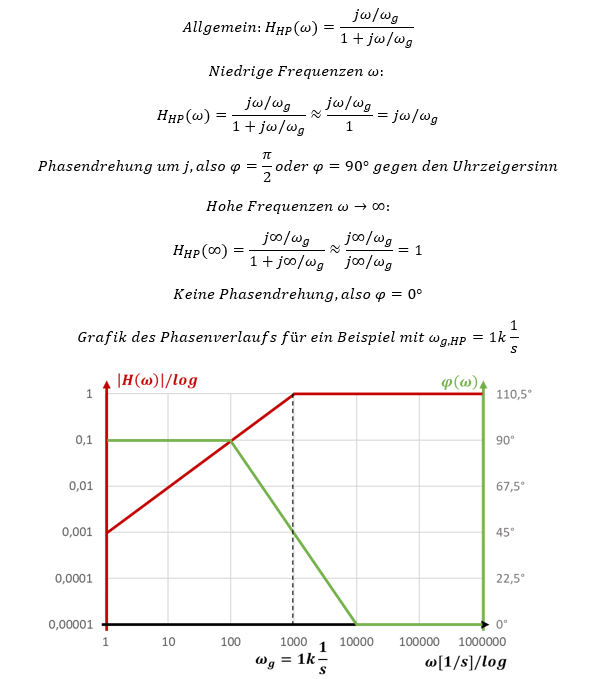
Die Phase ändert sich erneut rund um die Grenzfrequenz herum. Mit der Bode-Näherung für die Phase erhalten wir einen linearen Verlauf zwischen φ = 90° bei niedrigen Frequenzen bis φ = 0° bei hohen Frequenzen.
Hochpass mit Spule und Widerstand
Ich habe immer davon gesprochen, dass Filter auch mit Spule realisiert werden können. Das möchte ich einmal an einem Hochpassfilter zeigen. In der Praxis der Messtechnik nutzen wir eher Kondensatoren, weil diese billiger und kleiner sind und Spulen andere Schaltungsteile durch ihr Feld stören.
Alle Schaltungen, deren Übertragungsfunktion Hochpass-Verhalten zeigt, wirken auch als Hochpass. Wir suchen also eine Schaltung mit Spule und Widerstand, die folgendes Verhalten zeigt:
Widerstände und Kondensatoren verhalten sich in vielen Eigenschaften Reziprok. Wenn Sie ein Tiefpass-Filter aus Widerstand und Kondensator bauen und den Kondensator durch eine Spule ersetzen, dann erhalten Sie ein Hochpass-Filter.
Auslegen der Grenzfrequenz
Die Grenzfrequenz muss so gelegt werden, dass das Nutzsignal nahezu unverändert das Filter passiert, und dass die Störung möglichst stark gedämpft wird. Dafür legen wir beim Hochpass die Grenzfrequenz um Faktor 10 unter die Nutzfrequenz. Achtung: beim Tiefpass ist es genau anders herum!
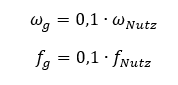
Aktives Hochpassfilter
Alle Schaltungen, deren Übertragungsfunktion sich zu dem Term
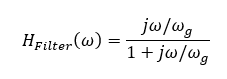
umformen lassen, sind Hochpass-Filter. Dieses Verhalten wird in folgender Verstärkerschaltung erreicht:
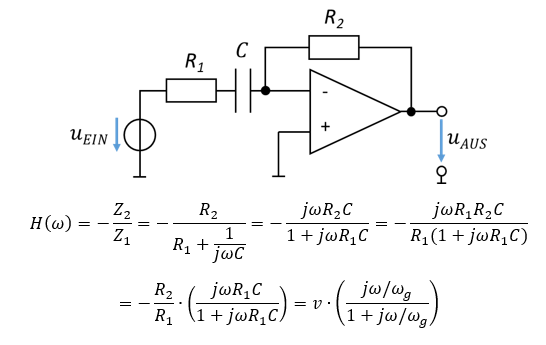
Im ersten Umrechnungsschritt wurde der Bruch wieder mit jωC erweitert. Anschließend habe ich den Bruch mit R1 erweitert. Danach habe ich die Verstärkung R2 / R1 aus dem Bruch nach vorne gezogen.
Jetzt erkennen Sie einen Term für die frequenzunabhängige Verstärkung v=-R2 / R1 und das Filter mit der Grenzfrequenz ωg=1/R1C. Die Schaltungsstruktur realisiert Verstärkung und Hochpass-Filterung. Die Intensität der Verstärkung und die Grenzfrequenz des Filters werden durch die Werte der Bauelemente bestimmt, die Sie gezielt für Ihre Anwendung festlegen.
Merke: Die Komponenten, die zwischen Spannungsquelle und invertierendem Eingang sitzen, bestimmen bei dieser Schaltung die Grenzfrequenz. Es ist in der Reihenschaltung egal, ob der Kondensator links oder rechts vom Widerstand R1 verbaut wird.
Aufgabe
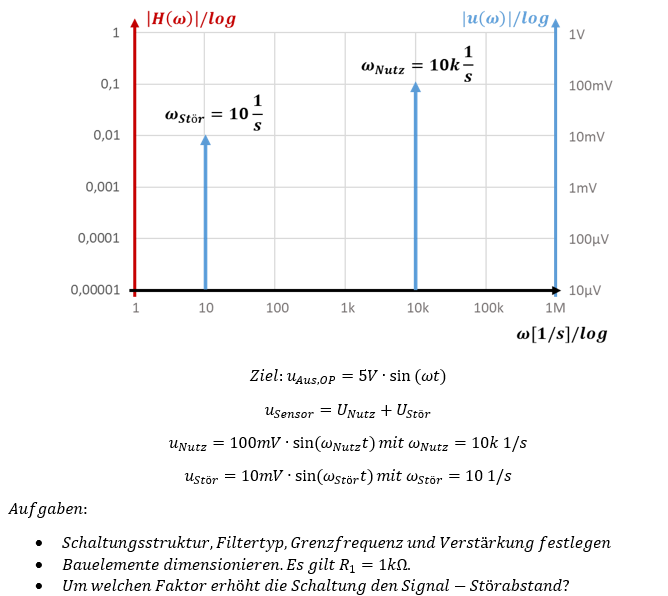
Lösung
Die Verstärkung wird für das Nutzsignal ausgelegt. 100mV müssen auf 5V verstärkt werden, dafür brauchen wir Faktor 50. Damit benötigen wir einen Verstärker und keine passive Lösung. Die Verstärkung beim invertierenden Verstärker für Filter beträgt dann v = -50. Das Vorzeichen stört bei Sinus-Größen nicht, es dreht nur die Phase um 180°.
Die Störfrequenz ist kleiner als die Nutzfrequenz, also brauchen wir ein (aktives) Hochpass-Filter. Beim Hochpass-Filter wird die Grenzfrequenz Faktor 10 unter die Nutzfrequenz gelegt, in diesem Beispiel also auf 1k 1/s.
Damit gehen wir in die Dimensionierung. Das Bode-Diagramm zeichne ich direkt für die ganze Schaltung, ich ziehe also die Verstärkung von v = -50 (Achtung: Betrag!) in die linke Achse mit rein:
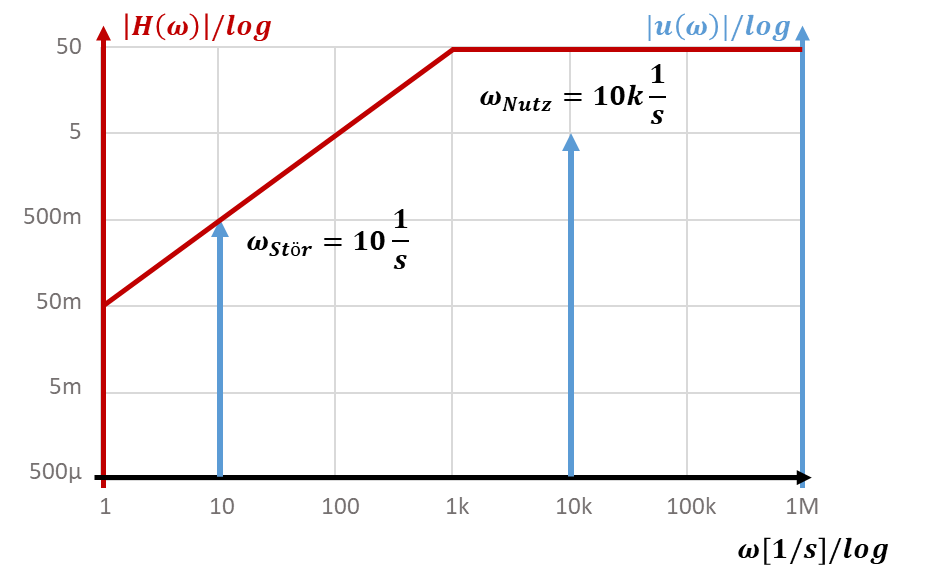
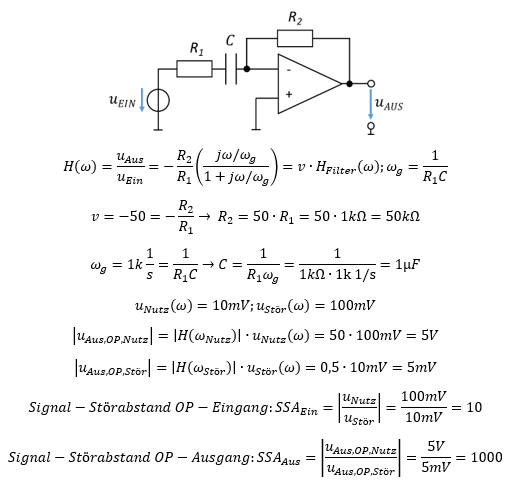
Die Schaltung erhöht den Signal-Störabstand von 10 auf 1000, also um Faktor 100.
Weiter