Ein Tiefpass-Filter wird mathematisch beschrieben als
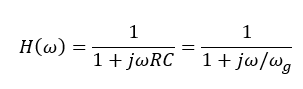
Elektrische Schaltungen, die sich nach dieser Formel verhalten, weisen Tiefpass-Charakteristik auf. Sie haben im letzten Kapitel schon ein passives Tiefpassfilter aus Widerstand und Kondensator kennengelernt. Ein passives Filter kann nur Spitzenwerte reduzieren, aber nicht erhöhen. Aktive Filter können Signale verstärken und dämpfen.
Die folgende Schaltung kombiniert einen invertierenden OP-Verstärker mit einem Tiefpass-Filter.
Bisher haben wir nur Widerstände an OP-Schaltungen betrachtet. Für Filter brauchen wir aber Speicher. Deshalb betrachten wir an Stelle der Widerstände jetzt komplexe Impedanzen. Es gilt:
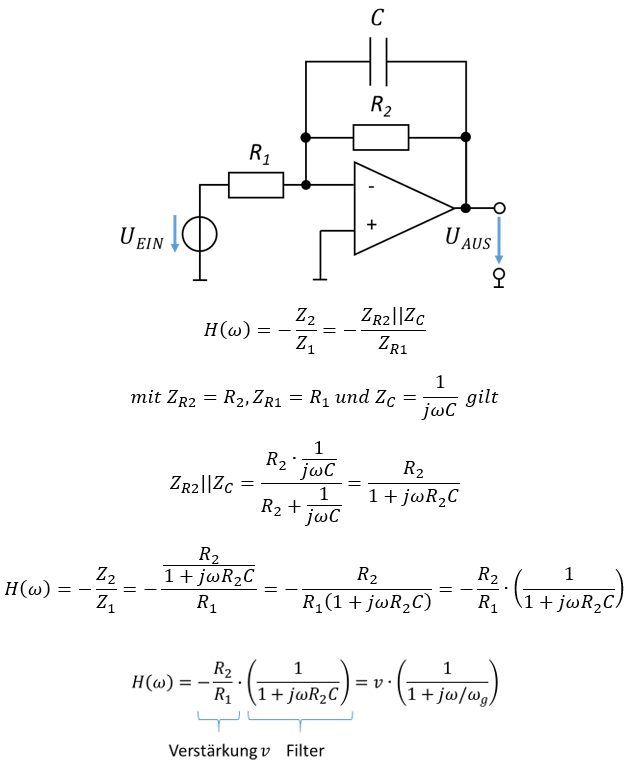
Die Übertragungsfunktion besteht aus dem Verstärkungsterm des klassischen invertierenden Verstärkers multipliziert mit der Übertragungsfunktion eines Tiefpasses.
Die Verstärkung v wird durch die beiden Widerstände festgelegt. Die Grenzfrequenz wird von den Bauelementen zwischen OP-Ausgang und invertierendem Eingang bestimmt: Von R2 und C. Es gilt für die obere Schaltung:
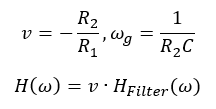
Beispiel
Ein Sensorsignal setzt sich aus einem Nutzanteil (abhängig von der physikalischen Größe) und einem Störanteil zusammen. Es gilt:
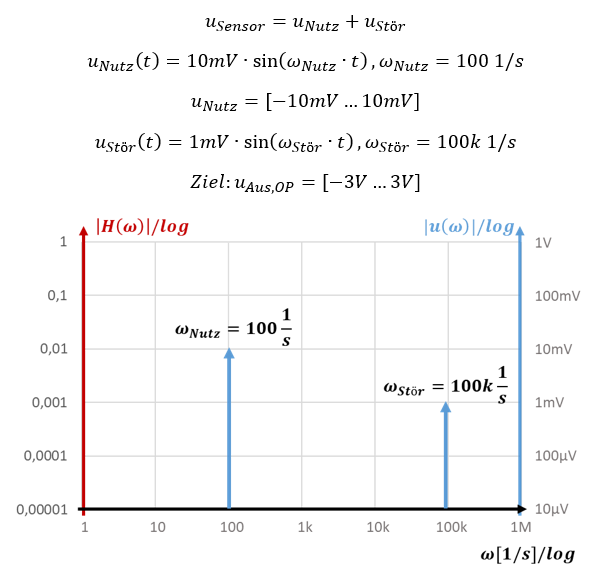
Bei Filter-Aufgaben ignorieren wir zunächst das Verschieben und Verstärken von Signalen, wir betrachten nur die Verstärkung. Das reduziert die Komplexität und macht reale Aufgaben einfacher zu berechnen. Wir reduzieren noch weiter: Es wird nur der Betrag der Verstärkung betrachtet, nicht das Vorzeichen und keine Phasendrehung mit j.
Aufgabe: Zeichnen und dimensionieren Sie eine Schaltung, mit der das Nutzsignal optimal auf den Ziel-Spannungsbereich abgebildet wird und die Störung maximal gedämpft wird. Setzen Sie R2=300kΩ.
Lösung: Zunächst berechnen wir die notwendige Verstärkung. Mit v = +300 oder v = -300 wird der Bereich der Nutzspannung richtig auf den Bereich der Ausgangsspannung abgebildet. Sie können beide Bereichsgrenzen des Nutzsignals mit den Faktoren multiplizieren und erhalten jeweils die Bereichsgrenzen des Ausgangssignals. Zwei Lösungen sind möglich. Da Filter in diesem Tutorial immer mit invertierenden Verstärkern aufgebaut werden, wählen wir v = -300.
Die Grenzfrequenz legen wir um Faktor 10 höher als die Nutzfrequenz auf ωg=1k 1/s.
Wir realisieren diese mathematische Funktion mit der folgenden Filterschaltung:
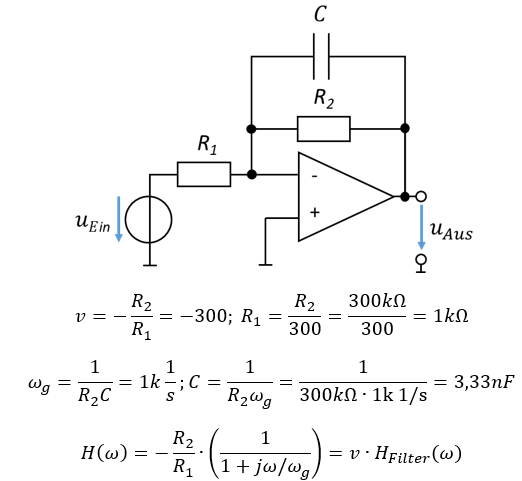
Aus dem Quotienten der Widerstände errechnen Sie die Verstärkung. Aus den Bauelementen über dem OP berechnen Sie die Grenzfrequenz.
Die Berechnung der Verstärkung bzw. Dämpfung der beiden Signale kann aus der Übertragungsfunktion berechnet werden. Alternativ kann sie – viel einfacher – aus dem Bode-Diagramm abgelesen werden.
Berechnung der Übertragungsfunktion
Die Übertragungsfunktion setzt sich aus Filterung und Verstärkung zusammen.
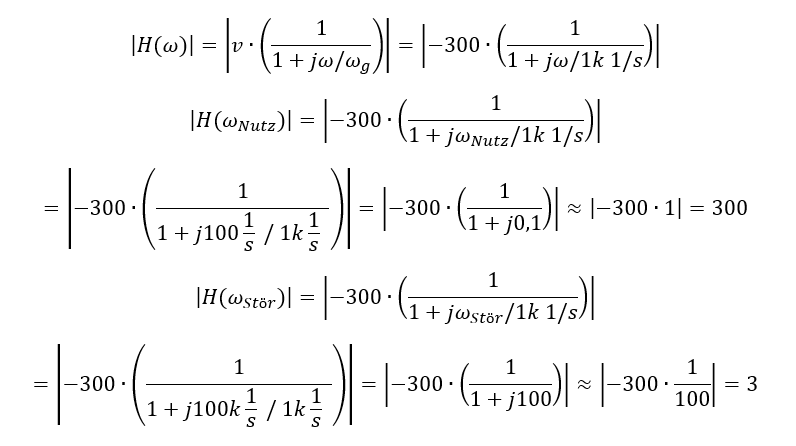
Die Berechnung ist möglich, aber mathematisch aufwändig. Sie können alternativ das Bode-Diagramm auf zwei Arten benutzen:
Trennung von Verstärkung und Filterung
Wir betrachten das Bode-Diagramm nur für die Filterung, nicht für die Verstärkung. Am Ende müssen wir das Ergebnis der Filterung noch mit der Verstärkung multiplizieren. Es gilt für alle Signale v = -300. Je nach Frequenz gilt zusätzlich für die Signale folgendes Bode-Diagramm nur des Filters:
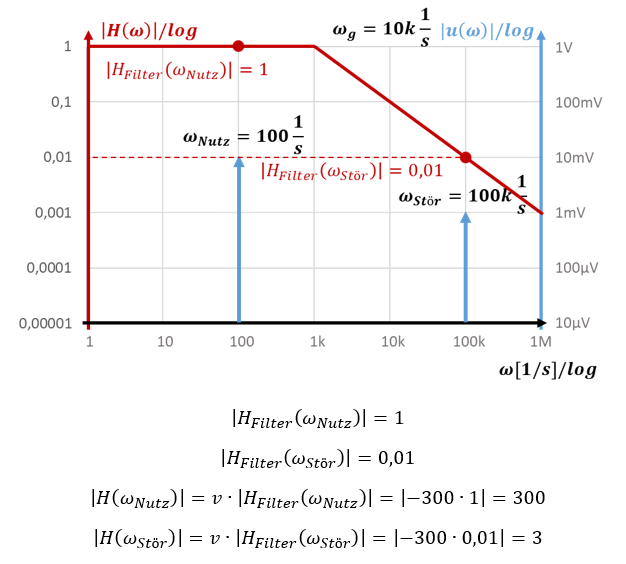
Der Betrag der Übertragungsfunktion |HFilter(ω)| bei einer Frequenz ω kann als y-Wert abgelesen werden. Beide Signale werden mit v verstärkt. Das Nutzsignal wird dann vom Filter mit 1 verstärkt (durchgelassen) und das Störsignal wird mit 0,01 verstärkt oder um Faktor 100 gedämpft.
Verstärkung und Filterung in einem Schritt
Es geht auch in einem Schritt: Die Verstärkung v wird in das Bode-Diagramm integriert. Dafür wird das Bode-Diagramm von |H (ω)| statt nur von |HFilter(ω)| gezeichnet. Es ändert sich die Skalierung der linken y-Achse. Sie können direkt Verstärkung und Filterwirkung in einem Schritt aus dem Bode-Diagramm ablesen.
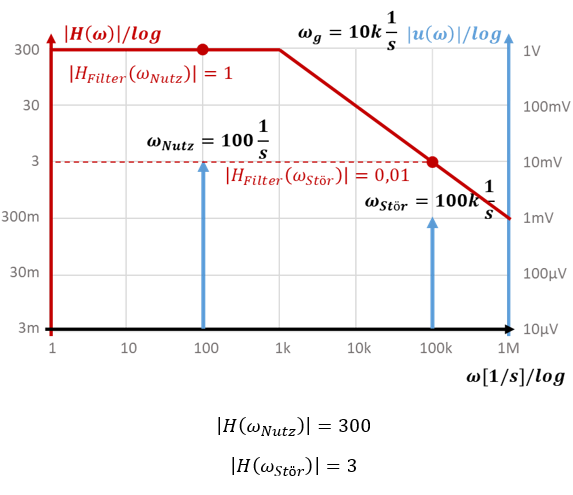
Um die Verstärkung v ins Bode-Diagramm hineinzuziehen, wird die y-Achse mit dem Betrag der Verstärkung v multipliziert. Beide vorgestellte Verfahren sind gleichwertig. Auch in der Prüfung geben sie die gleichen Punkte.
Signal-Störabstand
Ein wichtiges Maß für die Beurteilung eines Filters ist der Signal-Störabstand. Er beschreibt, wie stark ein Nutzsignal durch eine Störung beeinflusst wird. Mathematisch gibt er an, um wieviel der Spitzenwert des Nutzsignals größer ist als der Spitzenwert des Störsignals. Ein großer Wert des Signal-Störabstands ist also gut. Den Signal-Störabstand erhalten wir aus dem Betrag der Quotienten der Spitzenwerte. Betrachten wir dafür die Spitzenwerte oder die Beträge der Eingangs- und Ausgangssignale. Betrachten wir dafür wieder das Beispiel von weiter oben:
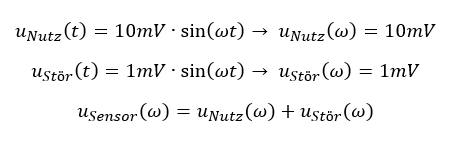
Am Ausgang des OPs gilt:
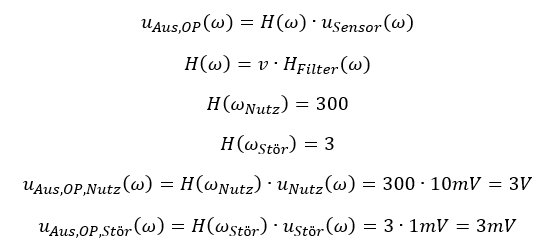
Die komplexe Form des Signals als Funktion von ω gibt direkt den Spitzenwert aus. Aus 1mV Störsignal-Spitzenwert wird am Ausgang des OPs 3mV. Aus 10mV Nutzsignal-Spitzenwert wird 3V. Das Nutzsignal wird viel mehr verstärkt als das Störsignal. Wir können den Signal-Störabstand (SSA) in der Sensorspannung und am Ausgang des OPs berechnen um zu ermitteln, wie gut die Schaltung ihre Arbeit macht:
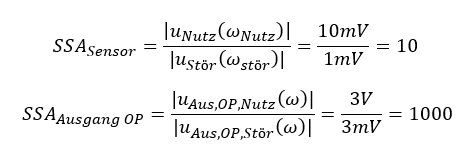
Der „Abstand“ zwischen Nutz- und Störsignal wird durch die Schaltung um Faktor 100 größer. Betrachten wir solch eine gute „Störunterdrückung“ um Faktor 100 in einem Zeitverlauf, sieht das so aus:
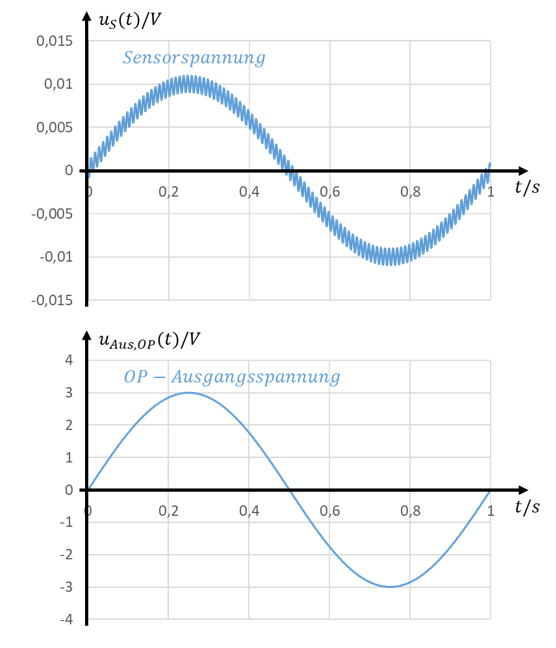
Tiefpassfilter können auch mit Spulen als Speicher aufgebaut werden. In der Messtechnik werden in OP-Schaltungen Kondensatoren bevorzugt, weil sie den Rest der Schaltung nicht durch Streufelder stören und deutlich günstiger und kleiner als Spulen sind.
Passive Tiefpass-Filter werden nur aus passiven Bauelementen – also Spulen, Kondensatoren und Widerständen – aufgebaut. Diese Filter können die Amplitude von Signalen nur dämpfen oder passieren lassen. Soll ein Signal gleichzeitig verstärkt werden, müssen aktive Filter mit OP-Schaltungen genutzt werden. Wenn ein Signal sowieso verstärkt werden soll, ist es sehr einfach, dieses zusätzlich zu filtern. Sie müssen dafür nur einen Kondensator hinzufügen.
Beachten Sie: Die Grenzfrequenz und die Verstärkung hängen nicht von der Schaltungsstruktur ab. Diese Parameter stellen Sie durch die Bauelemente ein. Deshalb sind Verstärkung und Grenzfrequenz in beiden Schaltungen nur Beispiel-Werte.
Weiter