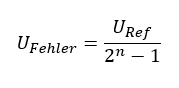In der Abbildung unten folgt zur Veranschaulichung ein Beispiel für das Verhalten eines 3 Bit ADCs mit UREF = 3V bei einem sinusförmigen Eingangsspannungssignal mit u(t) = 1,5V + 1,5V ∙ sin(ωt) mit f = 0,8Hz.
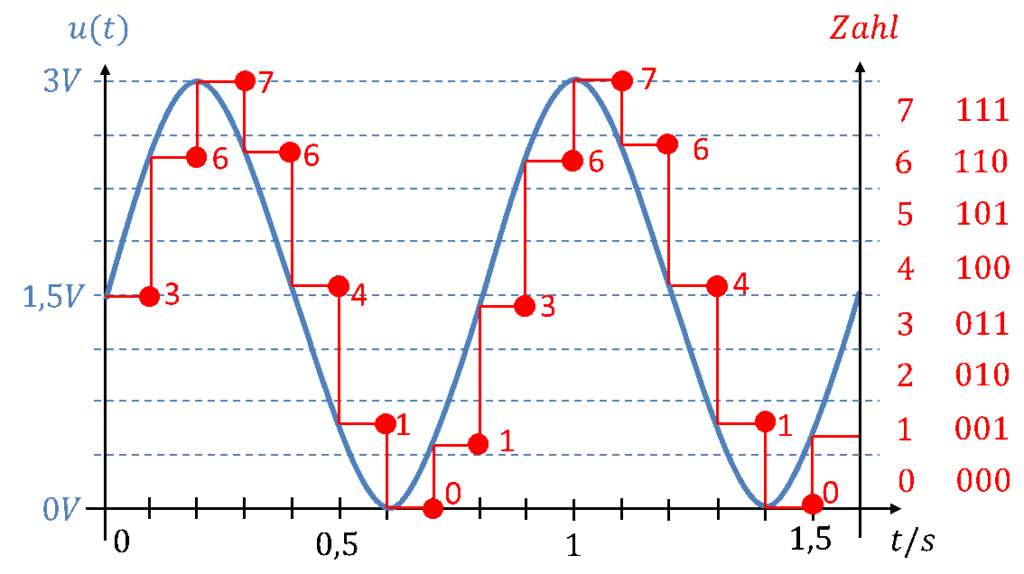
In der Darstellung werden zwei Y-Achsen verwendet. Betrachten wir zunächst nur die blaue Kurve und die linke Achse. In blau ist der Spannungsverlauf über der Zeit gezeichnet. Es handelt sich um eine um 1,5V nach oben verschobene Sinusfunktion mit dem Spitzenwert 1,5V. Die Frequenz beträgt f = 1,25Hz, denn eine Periode des Sinus ist nach der Periodendauer T = 0,8s abgeschlossen.
Der ADC beginnt eine Wandlung immer bei der Zeit, bei der ein schwarzer senkrechter Strich auf der Zeitachse zu sehen ist. Er hält diesen Wert für die Dauer einer Umwandlung intern konstant. Dies deuten die roten waagerechten Striche an. Nach der Umwandlungsdauer gibt der ADC eine Zahl aus. Diese Zeitpunkte sind mit roten Punkten markiert.
Die rote Zahl neben den Punkten zeigt die Zahl an, die der ADC ausgibt. Liegt die Eingangsspannung zwischen zwei waagerechten gestrichelten blauen Linien, wird die Zahl ausgegeben, die rechts an der zweiten Y-Achse aufgetragen ist. Liegt die Spannung z. B. zwischen der Zeitachse (0V) und der untersten waagerechten gestrichelten Linie, gibt der ADC eine 0 als Zahl aus. Neben den Dezimalzahlen sind ganz rechts die zugehörigen Dualzahlen angegeben.
Der ADC gibt immer zu festen Zeitpunkten ganze Zahlen aus. Es wird deutlich, wie viel Information in der Amplitude dadurch verloren geht, dass die Anzahl der Zahlen begrenzt ist, und feine Unterschiede zwischen Spannungsamplituden nicht unterschieden werden können. Im zeitlichen Verlauf der Spannung geht viel Information dadurch verloren, dass die Abstände zwischen den Umwandlungszeiten so lang sind.
Wenn die analoge Signalverarbeitung die Sensorspannung nicht gut auf die ADC-Eingangsspannung abbildet, dann ist die Signalspannung z. B. viel kleiner als die Referenzspannung. Es tritt folgender Effekt auf:
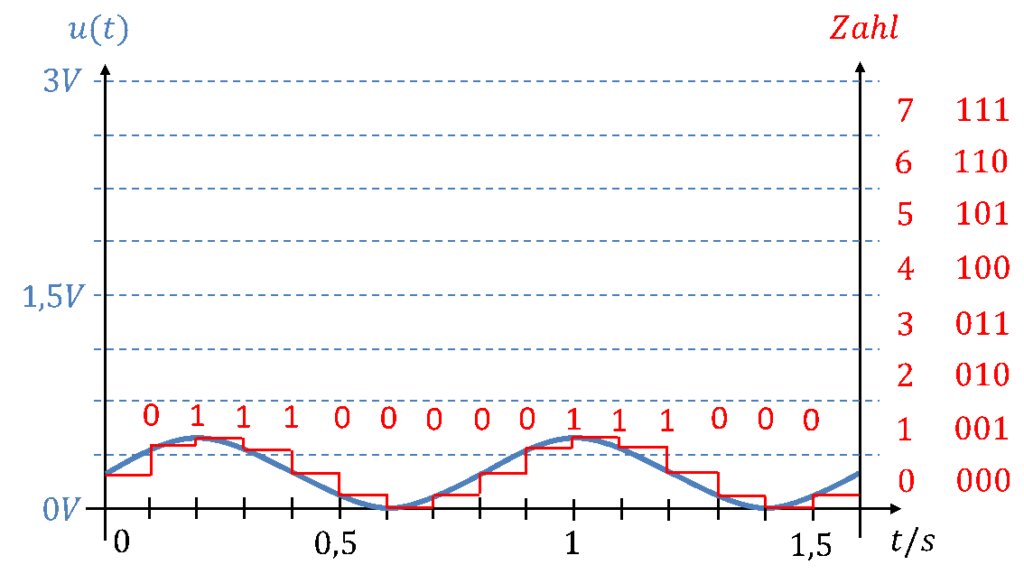
Die Spannung ändert sich nur so wenig, dass nur das unterste Bit seinen Wert ändert. Alle anderen Bits bleiben unverändert bei 0. Aus dem Zahlenstrom über der Zeit lässt sich nicht mehr ausreichend gut rekonstruieren, wie das analoge Signal ausgesehen hat.
Die Aufgabe der analogen Signalverarbeitung liegt deshalb darin, ein Sensorsignal so aufzubereiten, dass es möglichst den Eingangsspannungsbereich des ADCs zwischen 0V und UREF vollständig ausfüllt. Dann entspricht das digitale Signal möglichst gut dem analogen Signal.
Die effektiv wirksamen Bits sind nur die, die bei Änderung der Eingangsspannung auch ihren Wert ändern. Im Beispiel oben ist nur eines der drei Bits wirksam. Wie sich die Anzahl der wirksamen Bits auf die Signalqualität auswirkt zeigt die folgende Abbildung für 3 Bits, 5 Bits und 8 Bits.

Bei mehr als 8 Bits wird das Signal immer noch besser, der Effekt ist in einem solchen Diagramm aber schon mit dem Auge nicht mehr sichtbar. Das Digitalisieren erhöht immer die Messunsicherheit. Die Auflösung des ADCs in der Messkette muss so gewählt werden, dass die Messunsicherheit noch innerhalb der Spezifikation liegt. Wenn Sie eine hohe Anforderung an Genauigkeit haben, dann brauchen Sie einen ADC mit hoher Bitzahl n.
Quantisierung
Angenommen ein ADC rundet immer ab. Der Fehler durch diese „Quantisierung“ ist dann im worst case etwas kleiner als 1. Eine 12,999 wird dann z. B. zu einer 12. Wenn die Eingangsspannung nur ganz wenig unterhalb einer Schaltschwelle liegt und abgerundet wird, dann entsteht durch das Runden der maximale Fehler. Auf die Eingangsspannung zurückgerechnet entsteht ein Fehler von