Sinusförmige Spannungsverläufe bezeichne ich in diesem Tutorial oft als „Signale“. Sie sind durch Spitzenwert, Frequenz und Phase charakterisiert. Sinusförmige Messwerte tragen die Intensität der physikalischen Größe oft im Spitzenwert oder in der Amplitude. In der Messtechnik interessiert der Spitzenwert mehr als die Phase, denn diese stellt nur eine Zeitverschiebung dar. Bei Messwerten ist es selten wichtig exakt zu wissen, zu welchem Zeitpunkt ein Messwert vorlag. Es ist oft wichtiger zu wissen, wie hoch der Messwert war.
Betrachten wir Töne und Musik zur Veranschaulichung von Wechselgrößen. Töne sind sinusförmige Größen. Sie werden in einem Smartphone durch sinusförmige Spannungen erzeugt. Die Spannung bringt einen Lautsprecher im Kopfhörer dazu, sinusförmigen Schall zu erzeugen. Die Tonhöhe wird durch die Frequenz des Signals bestimmt. Die Lautstärke des Tons entspricht seinem Spitzenwert.
Ein Filter ändert den Spitzenwert (und die Phase) eines Eingangssignals abhängig von der Signalfrequenz. Am Ausgang ist der Spitzenwert größer, unverändert oder kleiner als am Eingang. Lassen wir Musik durch ein Filter laufen, dass die Spitzenwerte hochfrequenter Signale reduziert. Die Musik am Ausgang des Filters klingt dumpf, denn alle hohen Töne (mit großer Frequenz) sind leiser geworden.
Durchläuft die gleiche Musik ein Filter, das die Spitzenwerte tiefer Frequenzen reduziert, klingt sie wie aus einer billigen Box. Der Bass ist am Ausgang des Filters leiser geworden. Bässe haben niedrige Frequenzen.
Unterschiedliche Frequenzen in der Messtechnik
Es ist schwierig, elektrische Größen irgendwie aus physikalischen Größen zu gewinnen. Oft sind die elektrischen Größen am Ausgang der Sensoren sehr schwach. Wenn es Wechselsignale sind, dann ist ihr Spitzenwert sehr klein. Wir bezeichnen das Sensorsignal als Nutzsignal.
Leider gibt es viele Störsignale, die von außen in das Messsystem eindringen. Störsignale werden i. A. zum Sensorsignal addiert. In der Praxis ist ein Nutzsignal immer von irgendeinem Störsignal überlagert. Ziel ist es, das Nutzsignal mit möglichst hohem Spitzenwert an den ADC-Eingang zu bringen. Die Spitzenwerte der Störsignale sollen möglichst gering sein. Sie sollen vor allem viel kleiner als der Spitzenwert des Nutzsignals sein.
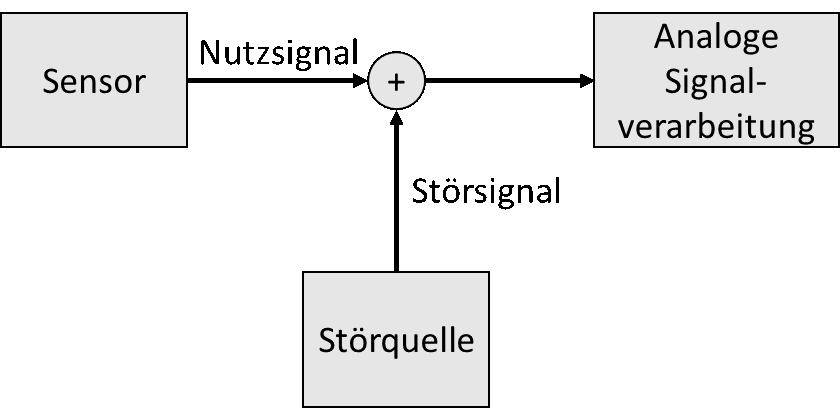
Wird ein Signal gedämpft, dann wird sein Spitzenwert kleiner. Wird es verstärkt, dann wird sein Spitzenwert größer. Filter werden genutzt, um störende Signale zu dämpfen.
Filter dämpfen oder verstärken Signale je nach Signalfrequenz unterschiedlich stark. Sind die Frequenzen des Nutzsignals und der Störsignale bekannt, können Filter so aufgebaut werden, dass die Störsignale gedämpft werden und das Nutzsignal sogar verstärkt wird.
Filter, mit denen Signale beeinflusst werden, bekommen im Deutschen den Artikel „das“ Filter vorgesetzt. Bei einem Kaffee-Filter schreiben wir „der“ Filter. Wie beim Kaffeefilter werden einige Signale durchgelassen und andere zurückgehalten.
Beispiel
In der folgenden Abbildung wird die Überlagerung eines niederfrequenten Nutzsignals (blau) mit einem hochfrequenten Störsignal (rot) betrachtet. Als Nutzsignal wird das Signal des menschlichen Herzschlags genutzt, dessen Frequenz im Bereich f = [1Hz … 3Hz] liegt. Das entspricht 60 bis 180 Schlägen pro Minute. Das Signal des Herzschlags weist am Ausgang des Sensors einen Spitzenwert von nur wenigen Millivolt auf. Wir sind froh, dass hier überhaupt ein Nutzsignal anliegt.
Das Herz-Signal (Puls) wird vom Netzbrummen überlagert. Das Netzbrummen ist eine Störung aus der Steckdose, die als Wechselspannung mit f = 50Hz und kleinem Spitzenwert wirkt. Es tritt an allen Messsystemen auf, die an einer Steckdose betrieben werden.
In der unteren Abbildung sind als Nutzsignal der Herzschlag (blau) und als Störsignal das Netzbrummen (rot) als getrennte Signale über der Zeit dargestellt. Das Herzsignal ist als Sinus mit f = 2Hz angenähert worden.
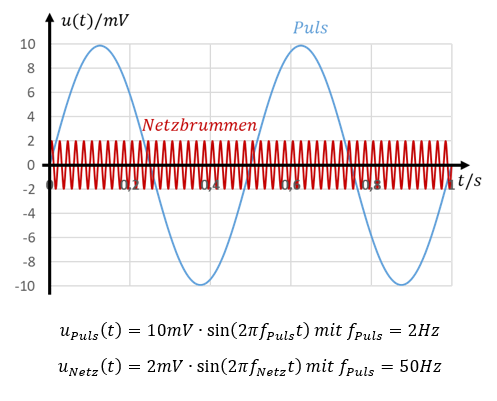
Werden beide Signale addiert, ergibt sich das grüne Signal in der folgenden Abbildung. In diesem Signal ist der Herzschlag zwar enthalten, das Signal ist aber ungeeignet z. B. für die Visualisierung beim Arzt oder im Krankenhaus.
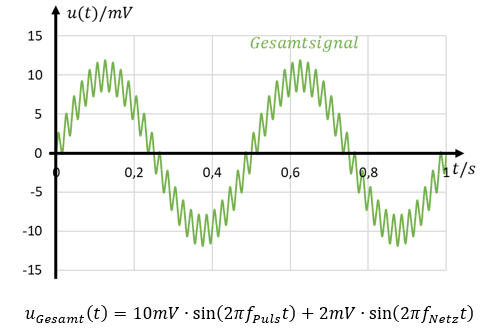
Die Aufgabe einer Filterschaltung besteht darin, das blaue Nutzsignal aus dem grünen Gesamtsignal wieder zu rekonstruieren. Dafür wird das Nutzsignal unverändert gelassen und der Spitzenwert des Störsignals reduziert.
Nehmen wir das Ergebnis vorweg: Wir haben irgendwie eine Filterschaltung realisiert, die das Störsignal bei f = 50Hz um Faktor 10 dämpft. Der Spitzenwert des Störsignals beträgt am Ausgang des Filters dann noch 0,2mV. Das Nutzsignal bei f = 2Hz lässt die Schaltung unverändert passieren. Am Ausgang dieses Filters sieht der Verlauf des Signals wieder ähnlich dem blauen Verlauf in der ersten Abbildung aus. Das gefilterte Signal ist in der unteren Abbildung dargestellt:
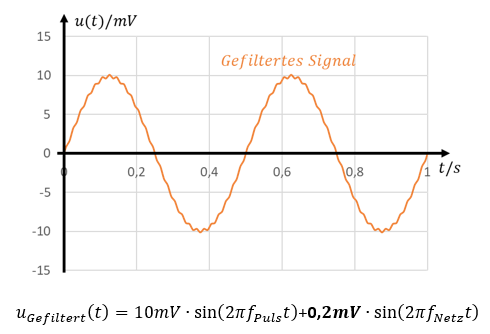
Je besser der Spitzenwert des Störsignals reduziert wird, desto besser kann die Signalform des Nutzsignals aus dem Gesamtsignal rekonstruiert werden. Im letzten Signalverlauf können wir den Verlauf des Herzschlags wieder ausreichend gut erkennen.
Ziel der Filterung von Signalen
Wenn ein Nutzsignal von einem Störsignal überlagert wird, wollen wir in der Messtechnik das Nutzsignal digitalisieren, das Störsignal aber nicht. Dafür wollen wir das Nutzsignal möglichst gut verstärken und das Störsignal möglichst stark reduzieren. Alle Schaltungen, die Sie bisher kennengelernt haben, behandeln alle Signale gleich, die aus einer gemeinsamen Quelle kommen. Sie sind für die Lösung dieses Problems also nicht geeignet.
Wenn die Frequenzen von Nutzsignal und Störsignal sich unterscheiden, können wir Filter einsetzen. Diese erhöhen oder reduzieren den Spitzenwert von Wechselsignalen abhängig von ihrer Signalfrequenz.

In den folgenden Kapiteln geht es darum, wie Filterschaltungen anschaulich arbeiten und wie sie realisiert werden können.
Weiter