Ein Signalflussdiagramm besteht aus Funktionsblöcken, die miteinander durch Pfeile verbunden sind. Jeder Funktionsblock symbolisiert dabei einen abgrenzbaren Teil des Systems wie z. B. den Sensor oder ein Stück Software. Ein Funktionsblock weist Ein- und Ausgänge auf. Im einfachsten Fall weist er einen Eingang und einen Ausgang auf. Signale wie z. B. die Temperatur oder eine digitalisierte Zahl werden als Pfeile zwischen den Blöcken gezeichnet. Weist ein Pfeil in Richtung des Blocks handelt es sich um eine Eingangsgröße.
In der Messkette ist die „Physikalische Größe“ ein Eingangssignal, das vom Funktionsblock „Sensor“ in die Ausgangsgröße „Elektrische Größe“ umgewandelt wird. Es gibt verschiedene Sensoren, die unterschiedliche physikalische Größen verarbeiten, sie alle haben aber diese grundlegende Struktur gemein. Der Funktionsblock „Analoge Signalverarbeitung“ bekommt vom Sensor die elektrische Größe als Eingangssignal überreicht und wandelt diese in eine elektrische Spannung für den Analog-Digital-Wandler um. Aus diese Weise kann in der Messkette das Übertragen von Signalen durch Funktionsblöcke unabhängig von der konkreten technischen Realisierung abstrahiert werden.
Übertragungsfunktion
Die Übertragungsfunktion H eines Funktionsblocks beschreibt mathematisch dessen Verhalten. Es gilt

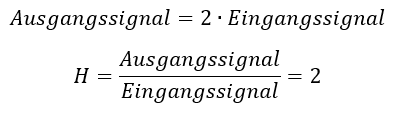
Mit der Information H=2 haben wir den Funktionsblock mathematisch vollständig beschrieben.
Das Ziel in der Analyse von Komponenten lautet, die Übertragungsfunktion H der Funktionsblöcke zu ermitteln. Das erreichen Sie z. B. durch Vermessen der Funktionsblöcke. Wenn Sie unterschiedliche Eingangssignale anlegen und die Ausgangssignale messen, dann können Sie den Funktionsblock charakterisieren.
Nehmen wir als Beispiel einen Sensor, der eine Stoffkonzentration C in einer Flüssigkeit misst.
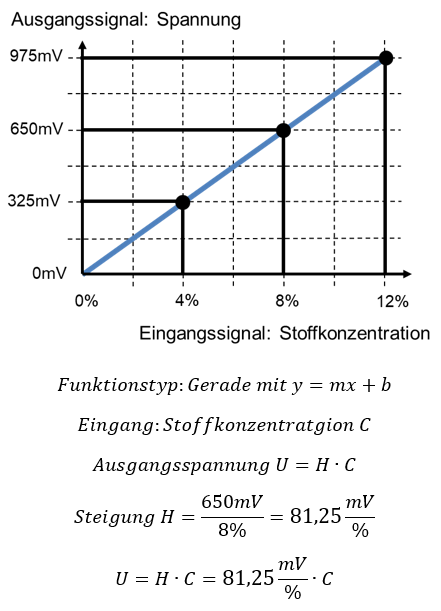
Das Ausgangssignal des Sensors ist eine Spannung. Die Übertragungsfunktion kann aus der Kennlinie des Sensors abgelesen werden. In der Kennlinie ist die Ausgangsgröße eines Funktionsblocks auf der Y-Achse über der Eingangsgröße auf der X-Achse aufgetragen. Die Steigung entspricht der Übertragungsfunktion H.
Setzt man die Eingangsgröße in die Gleichung ein, ergibt sich die Ausgangsgröße. Setzt man im Beispiel also eine Konzentration in die Gleichung ein, ergibt sich eine Spannung:
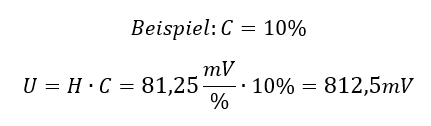
Die Einheit der Übertragungsfunktion ist die Einheit der Ausgangsgröße geteilt durch die Einheit der Eingangsgröße. Um den Funktionsblock vollständig zu beschreiben definieren wir im Blockdiagramm den Konzentrationssensor so:
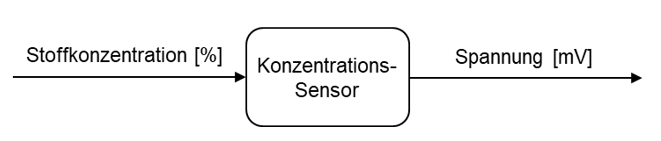
Sinn der Übertragungsfunktion
Warum macht die Angabe einer Übertragungsfunktion Sinn? Weil damit das Verhalten eines Gesamtsystems einfach aus dem Verhalten der darin enthaltenen Funktionsblöcke ermittelt werden kann. Nehmen wir als Beispiel ein System, das aus drei Funktionsblöcken besteht. Die Funktionsblöcke sind hintereinandergeschaltet.
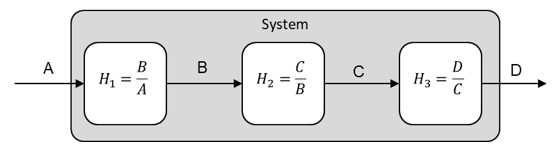
Der Eingang des Gesamtsystems ist das Signal A, am Ausgang liegt das Signal D an. Das Verhalten der drei Funktionsblöcke wird durch deren Übertragungsfunktionen H1 bis H3 beschrieben. Dann gilt
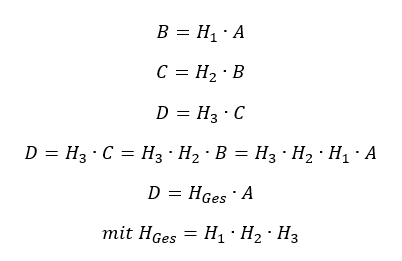
Wir müssen uns bei der Analyse des Verhaltens des gesamten Systems nicht mehr mit den Signalen innerhalb des Systems auseinandersetzen, wir können das Verhalten des Systems einfach über die Übertragungsfunktionen der Funktionsblöcke beschreiben. Dafür fassen wir die Übertragungsfunktionen der Funktionsblöcke zu einer Gesamt-Übertragungsfunktion zusammen, indem wir die sie multiplizieren.
Wenn Sie später ein Messsystem aus Funktionsblöcken zusammensetzen, dann können Sie die Funktionsblöcke anhand ihrer Übertragungsfunktionen auswählen, so dass Sie insgesamt das gewünschte Verhalten zwischen Eingangssignal A (physikalische Größe) und Ausgangssignal D (Ausgabe des Messwerts) bekommen.
Bitte behalten Sie diese Anwendung der Übertragungsfunktion im Hinterkopf. Sie werden in diesem Tutorial für alle Schaltungen Übertragungsfunktionen ermitteln, die die Änderung eines Signals zwischen Ausgang und Eingang beschreiben. Die Übertragungsfunktion beschreibt mathematisch, was ein Funktionsblock mit einem Eingangssignal anstellt, also wie es dieses verändert. Beispiele sind
– Verstärken
– Dämpfen
– Verschieben
– Filtern
Auf die Bedeutung dieser Begriffe gehen wir später detailliert ein. Hier noch ein Beispiel für ein Messsystem mit dem oben beschriebenen Konzentrations-Sensor:
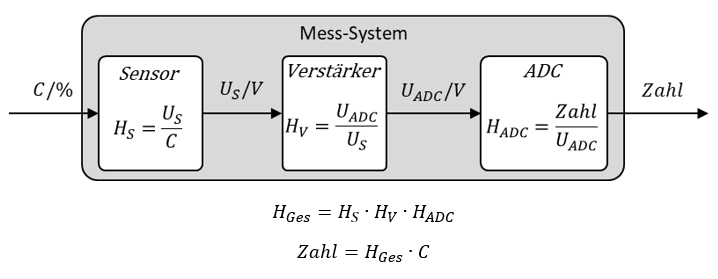
Es ist unerheblich, wie die Funktionsblöcke intern arbeiten. So lange Sie deren Übertragungsfunktionen kennen, können Sie die Ausgangsgröße zu einer physikalischen Größe berechnen, die nacheinander mehrere Funktionsblöcke durchläuft. Die Übertragungsfunktionen von Funktionsblöcken entnehmen Sie entweder den Datenblättern der Zukaufteile oder Sie berechnen Sie, wenn Sie selbst die Funktionsblöcke entwickelt haben.
Wofür ist die Gesamt-Übertragungsfunktion gut? Wenn die physikalische Größe am Eingang eines Mess-Systems sich ändert, dann gibt das System am Ausgang ständig neue Zahlen aus. Mit der Übertragungsfunktion können Sie errechnen, wie hoch die zugehörige physikalische Größe am Eingang ist, die Sie ja bestimmen wollen.
Zusammenfassung
Die Übertragungsfunktion H beschreibt mathematisch einen Funktionsblock, also z. B. einen Sensor. Wir ermitteln H, indem wir Eingangsgrößen an den Funktionsblock anlegen und die zugehörigen Ausgangsgrößen messen. Wenn wir die Ausgangsgröße über der Eingangsgröße zeichnen erhalten wir die Kennlinie des Funktionsblocks. Die Übertragungsfunktion ist die Steigung der Kennlinie.