Das gesamte Kapitel „Ungewollte Filter“ ist nicht prüfungsrelevant. Sie können es weglassen, wenn Sie sich nur schnell auf die Vorlesung vorbereiten wollen.
Betrachten wir Bewegungen im Alltag. Sie können einen Ball einmal pro Minute hochwerfen und fangen. Das schaffen Sie auch 10 Mal pro Minute. Wenn Sie das einmal pro Sekunde machen sollen, dann wird es schon eng. Je schneller Sie den Ball werfen und fangen, desto weniger hoch können Sie ihn werfen. Der Spitzenwert „Wurfhöhe“ sinkt also mit der Frequenz. Sie sind in der Fähigkeit, einen Ball hochzuwerfen und zu fangen, tiefpass-begrenzt.
Jedes System ist in allem irgendwann tiefpass-begrenzt. Nichts geht unendlich schnell. Dafür brauchen Sie nicht aktiv etwas zu filtern, das passiert ganz von alleine. Ein bewusst in ein System hinzugefügtes Filter ergänzt dieses natürliche Verhalten von Systemen.
Alle realen Schaltungen und Bauelemente weisen natürliches Tiefpass-Verhalten in ihrer Funktion auf. Die Signale am Ausgang eines Systems können sich nicht beliebig schnell ändern. Wir betrachten das Phänomen am Beispiel von Operationsverstärkern. Nehmen wir einen OP, der ein Eingangswechselsignal um Faktor v = -1000 verstärkt.
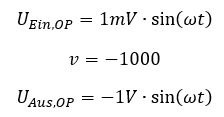
Der OP weist laut Datenblatt eine maximale Änderungsgeschwindigkeit seiner Ausgangsspannung aus: Die Slew-Rate (maximale Spannungssteigung). Ein OP mit einer Slew-Rate von 1V/µs kann seine Spannung um nicht mehr als 1V ändern, wenn wir ihm eine Mikrosekunde Zeit geben. Ein Signal mit einer Frequenz von f = 1MHz bewegt sich innerhalb einer Mikrosekunde mehrfach auf und ab. Setzen wir als Signalfrequenz für das Beispiel f = 1MHz ein und betrachten wir das Ausgangssignal des OPs:
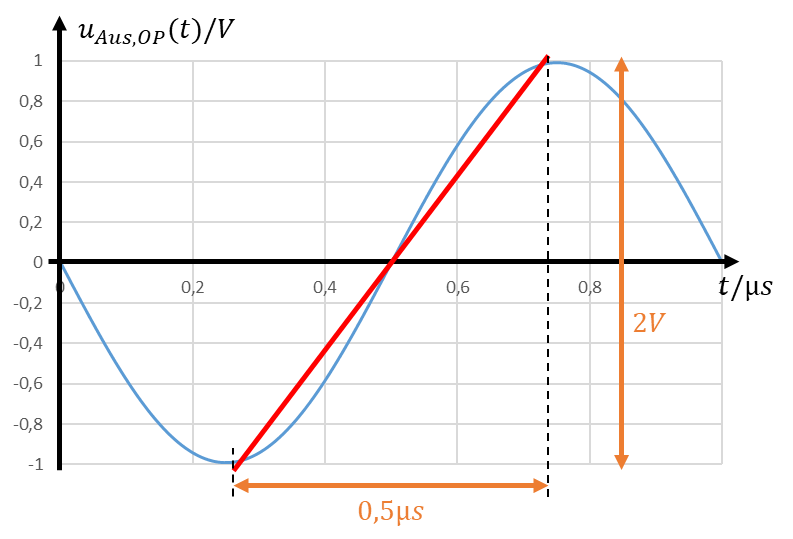
Das Ausgangssignal des OPs ändert sich zwischen den Zeitpunkten 0,25µs und 0,75µs um 1V. Wir tun mal so, als ob die Änderung linear verlaufen würde (roter Verlauf). Dann müsste der OP die Ausgangsspannung um 2V innerhalb von 0,5µs ändern. Das schafft er nicht, dafür ist sein Ausgang nicht schnell genug.
In der Analogie zum Wassermodell weist der OP am Ausgang ein Rohr mit einem begrenzten Durchmesser auf. Durch dieses Rohr passt nur eine begrenzte Wassermenge pro Zeit, also kann der Wasserstand am Ausgang des OP sich nicht beliebig schnell ändern.
Der OP kann dieses Ausgangssignal nicht erzeugen. Also erzeugt er das größte Signal, was er noch hinbekommt:
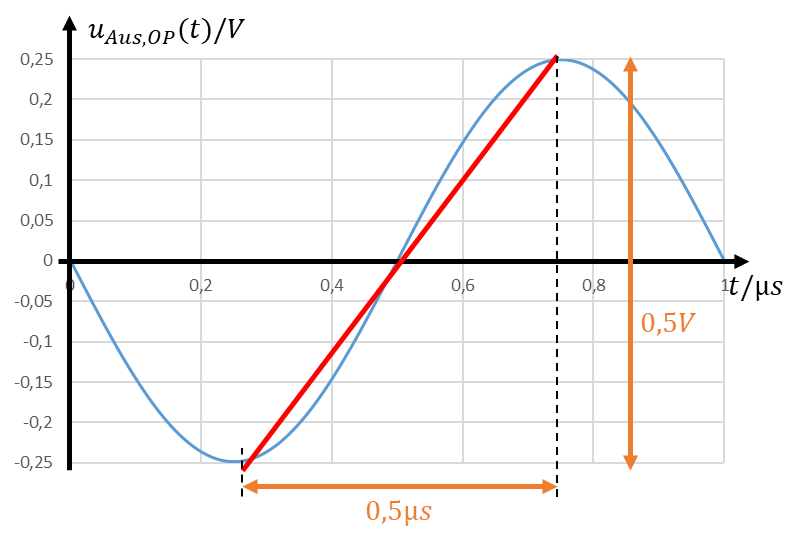
Betrachten wir eine Ausgangsspannung des OPs von 0,25V Spitzenwert. Wäre der Spannungsanstieg zwischen den Extremwerten der Ausgangsspannung linear, müsste der OP-Ausgang um 0,5V in 0,5µs ansteigen. Das bekommt er hin, denn er kann seinen Ausgang um 1V / µs ändern.
Je höher die Frequenz der Eingangsspannung ist, desto steiler ist der Spannungsanstieg bei gleichem Spitzenwert. Es bleibt weniger Zeit für den gleichen Spannungsanstieg, wenn die Periodendauer kleiner wird, weil die Frequenz steigt. Betrachten wir eine OP-Ausgangsspannung bei 10-fach höherer Frequenz. Der OP kann dann nur 1 / 10 der Ausgangsspannung stellen. Die Ausgangsspannung des OPs zeigt also Tiefpassverhalten, ohne dass jemand außen ein R oder C angeschlossen hat.
Verstärkungs-Bandbreite-Produkt
Es gibt mehr Einflussgrößen innerhalb eines OPs, die dessen Tiefpass-Verhalten bestimmen. Alle diese Effekte unterliegen einer Streuung oder Unsicherheit, ab wann sie wirken. Also hat ein OP zunächst Tiefpassverhalten mit einer Grenzfrequenz, die von vielen Effekten bestimmt wird und damit einen unsicheren Wert aufweist. Das ist Mist. Intern wird deshalb mit einem Widerstand und einem Kondensator ein dominantes Tiefpass-Filter erzeugt, dessen Grenzfrequenz vom Hersteller eingestellt wird. Diese Tiefpass-Grenzfrequenz des bewusst hinzugefügten Filters liegt im Bode-Diagramm weiter links als alle anderen natürlichen Grenzfrequenzen. Damit wird ein deterministisches und immer gleiches Verhalten aller OPs einer Baureihe sichergestellt.
Wenn der OP eine gewünschte Ausgangsspannung nicht mehr bereitstellen kann, dann sinkt effektiv seine Verstärkung. Die Verstärkung des OPs entspricht seiner Übertragungsfunktion H. Wir bei allen anderen Filtern liegt damit in der Übertragungsfunktion Tiefpass-Verhalten vor. Das kann folgendermaßen aussehen:
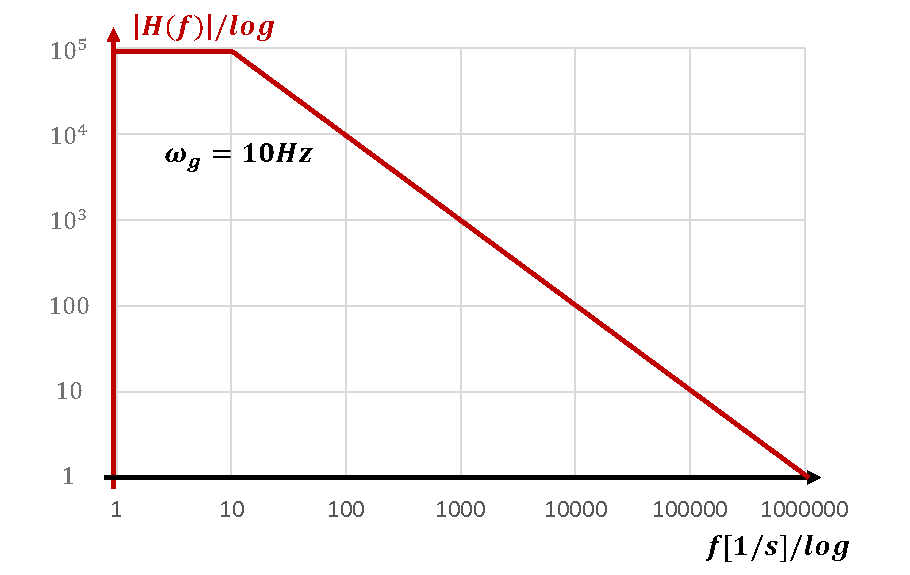
Dieser Beispiel-OP kann Gleichsignale mit einer maximalen Verstärkung von |v| = 100000 verstärken. Je größer die Signalfrequenz am Eingang ist, desto geringer ist die Verstärkung. Eingangssignale mit f = 1MHz werden nur noch mit |v| = 1 verstärkt. Der Frequenzbereich, bis zu dem eine gewünschte Verstärkung noch realisiert werden kann, wird als „Bandbreite“ bezeichnet. Dieser OP hat also eine Bandbreite von 1MHz, wenn wir z. B. v = -1 benötigen. Wenn dieser OP ein Eingangssignal mit v = -1000 verstärken soll, klappt das nur noch bis zu einer Signalfrequenz von 1kHz.
Das „Verstärkungs-Bandbreite-Produkt“ eines OPs ist eine Konstante, die im Datenblatt angegeben wird. Beim Beispiel-OP beträgt es 1MHz. Das Produkt aus Verstärkung und Bandbreite ist für jeden Punkt auf der roten Linie rechts von der Grenzfrequenz immer gleich 1MHz.
Der OP kann jeden Betriebspunkt unterhalb der roten Kurve bedienen. Die rote Linie begrenzt nur seine Verstärkung nach oben hin. Der OP kann z. B. bei f = 1kHz auch mit der Verstärkung v = 10 betrieben werden.
Dieses Tiefpass-Verhalten hat nicht direkt etwas mit der Slew-Rate von weiter oben zu tun. Mit dem Tiefpass-Verhalten aus dem Bode-Diagramm wird der OP künstlich verlangsamt, damit sein Verhalten deterministisch ist. Dafür muss die Grenzfrequenz des Tiefpass-Verhaltens so weit links im Bode-Diagramm liegen, dass alle anderen Effekte gar nicht erst wirken.
Das ist so, als ob sich durch das Tiefpass-Filter der Ball so langsam bewegen würde, dass Sie ihn immer locker fangen und werfen können. Der Ball fliegt dann z. B. mit der maximalen Frequenz f = 0,1 Hz. Niemand bemerkt dann, dass Sie den Ball nur bis zu einer Frequenz von f = 1Hz fangen und wieder werfen können. Sie kommen mit einer gezielten Verlangsamung der natürlichen Grenzfrequenz zuvor, so dass diese nach außen nicht mehr wirksam ist.
Weiter