Für die Beschreibung zufälliger Fehler betrachten wir kurz nicht weiter die Länge des Zollstocks als Fehlerquelle, die halten wir konstant. Stattdessen betrachten wir die Genauigkeit, mit der der Zollstock angelegt und abgelesen wird. Dieser Parameter ändert sich bei jeder Messung unabhängig von den vorherigen Messungen.
Wenn Sie mit einem idealen Zollstock, der exakt die Länge l = 2m aufweist, 10 Mal die Länge des gleichen Tisches messen, dann werden Sie voraussichtlich 10 unterschiedliche Ergebnisse bekommen, denn mal verrutscht der Zollstock etwas nach links und mal etwas nach rechts. Die wahre Länge des Tischs beträgt l = 73,05cm. Die 10 Ergebnisse werden zufällig verteilt rund um diesen Wert liegen. Folgende Messwerte könnten bei dem Experiment herauskommen:
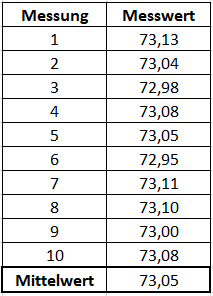
Die Messwerte werden auf der Y-Achse aufgetragen. Auf der X-Achse sehen Sie die einzelnen Messungen von 1 bis 10 aufgetragen.
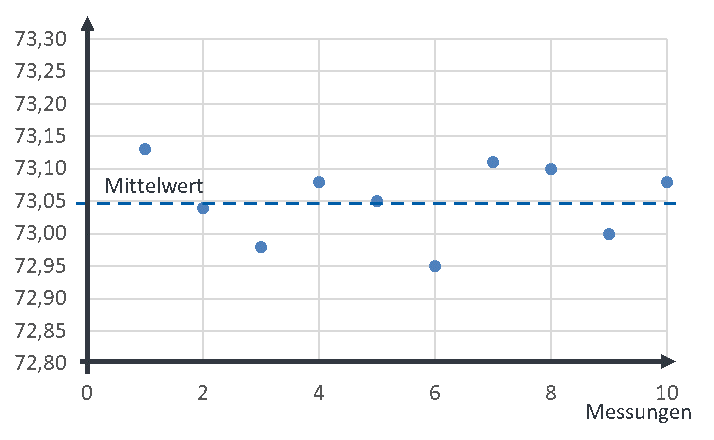
Der wahre Wert ist als gestrichelte Linie eingezeichnet. Wenn ausreichend viele Messungen durchgeführt werden, dann behaupten die Statistiker, dass der Mittelwert aller Messungen dem wahren Wert entspricht. Zufällige Abweichungen können wir also durch Bildung des Mittelwerts kompensieren. Wenn in einem Messsystem viele Messwerte nacheinander aufgenommen werden, unterscheiden diese sich immer voneinander. Wenn z. B. immer 100 aufeinander folgende Messwerte gemittelt werden, sieht der zugehörige Quellcode im Mikrocontroller folgendermaßen aus:
Summe_100_letzte_Werte = Wert1 + Wert2 + Wert3 + (…) + Wert100
Mittelwert = 0,01 ∙ Summe_100_letzte_Werte
Oft wird ein gleitender Mittelwert eingesetzt. Dabei wird immer der älteste Wert aus der Summe entfernt und ein neuer, gerade ermittelter Wert hinzugefügt. Das sieht dann folgendermaßen aus:
Summe_100_letzte_Werte = Summe_100_letzte_Werte – ältester_Wert + neuster_Wert
Mittelwert = 0,01 ∙ Summe_100_letzte_Werte
Der Mittelwert reduziert den Einfluss des Zufalls umso besser, je mehr Messwerte gemittelt werden. Es verbleibt immer ein Rest an Zufall bei einer Messung.
Weiter