im allgemeinen Regelkreis können mit linearen Gleichungen berechnet werden. Setzen wir einen Speicher für A ein und berechnen das Führungsverhalten und die Störunterdrückung.
Es gilt
Führungsverhalten
Damit gilt für das Führungsverhalten mit d = 0:
Multiplizieren wir Nenner und Zähle mit s, erhalten wir
Es bleibt der Parameter s für die Frequenz im Ergebnis enthalten. Ziel der Regelung ist HFü = 1, denn damit gilt y = w mit d = 0.
Interpretation von s
Den Parameter s können Sie sich wie eine Frequenz f vorstellen. Zwischen beiden liegt i. A. nur ein Faktor. Das Verhalten der Funktion ändert sich also mit der Frequenz, es verhält sich wie ein Filter aus der Messtechnik.Für die Interpretation des Verhaltens ziehen wir wieder die Sprungantwort heran. Wir setzen am Eingang des Systems einen Sprung im Sollwert w an und schauen uns an, wie der Ausgang y über der Zeit reagiert. Das Ergebnis wird nicht berechnet, sondern z. b. in Matlab Simulink simuliert. Die Simulation erfolgt in der Vorlesung, das Ergebnis nehme ich hier vorweg:
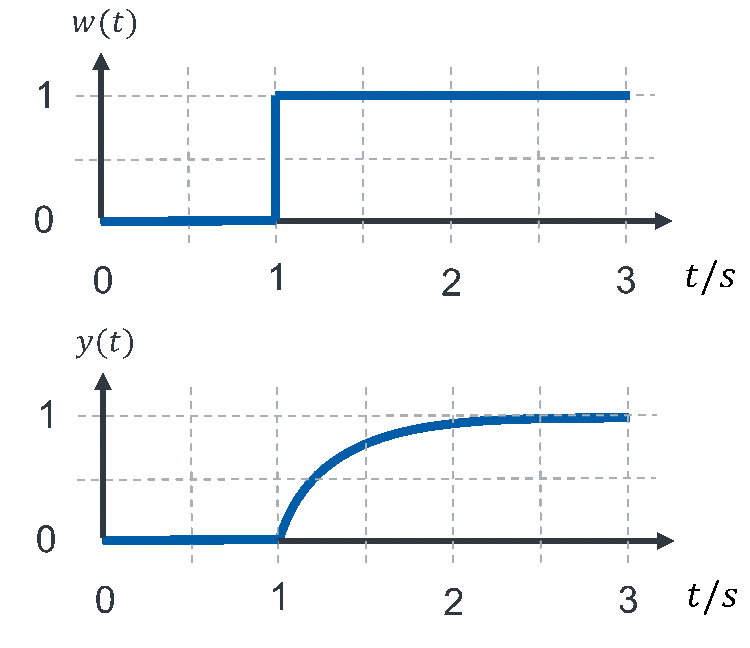
Diese Sprungantwort entspricht weder P-Verhalten noch I-Verhalten. Wir haben es also mit einer neuen Verhaltensweise namens „PT-1 Verhalten“ zu tun. Dieses Verhalten wird in einem späteren Kapitel besprochen. Setzen wir für A I-Verhalten ein, kommt im geregelten System kein I-Verhalten heraus. Wir analysieren das Verhalten hier zunächst an charakteristischen Zeitpunkten. Direkt nach dem Sprung in der Führungsgröße verändert sich die Ausgangsgröße exponentiell. Irgendwann ändert sich das Verhalten dann nicht mehr.
Wir analysieren das Verhalten zunächst nach unendlich viel Zeit im sogenannten „eingeschwungenen Zustand“, in dem sich der Verlauf nicht mehr ändert. In diesem Bereich ändert sich die Regelgröße y nicht mehr über der Zeit, sie ist also konstant. Ein konstanter Zeitverlauf weist eine Frequenz von f = 0 Hz auf. Wir können den Wert von y im eingeschwungenen Zustand also mit s = 0 1/s berechnen. Der Ausdruck
wird für s = 0 1/s zu HFü = 1. Damit gilt y = 1 ∙ w. Dies ist auch grafisch ersichtlich, denn der Verlauf von y(t) erreicht im eingeschwungenen Zustand den Wert y = 1 mit w = 1. Damit hat das System nach einiger Wartezeit das Ziel der Regelungstechnik ideal erreicht. Deshalb werden Speicher in der Regelungstechnik gerne eingesetzt.
Im Übergangsbereich, also dem Zeitbereich mit starker Änderung der Regelgröße y, gilt aber y ≠ w. Hier wird das Ziel der Regelung temporär nicht erreicht. Das Verhalten im Übergangsbereich wird als PT-1-Verhalten bezeichnet.
Die Übertragungsfunktion der Störunterdrückung mit I-Verhalten in Block A lautet:
mit w = 0.
Setzen wir
ein, ergibt sich
Multipliziert man Zähler und Nenner mit s, ergibt sich
Dies ist wieder ein neues Verhalten, es ist weder P-Verhalten, noch I-Verhalten noch PT-Verhalten. Wir analysieren erneut zunächst das Verhalten im eingeschwungenen Zustand. Ziel der Regelung ist HSu = 0, denn dann ist y unabhängig von d. Im eingeschwungenen Zustand gilt s = 0, also setzen wir s = 0 in die obere Gleichung ein.
Das Ergebnis ist erfreulich. Sobald A aus einem Speicher besteht, wirkt die Störung d nach einiger Zeit im eingeschwungenen Zustand überhaupt nicht mehr auf den Ausgang y.
Berechnung der Regelgröße
Aus beiden Übertragungsfunktionen zusammen kann die Regelgröße berechnet werden: Es gilt insgesamt unter Berücksichtigung von Führungsgröße w und Störgröße d:
Setzen wir s = 0 ein, kommt insgesamt das Ergebnis
y = w
heraus. Ein geregeltes System mit A bestehend aus einem Speicher erfüllt im eingeschwungenen Zustand alle bisher betrachteten Ziele der Regelungstechnik.
Beispiel
Es wird die Geschwindigkeitsregelung des Autos betrachtet. Ziel: Sie sollen vsoll=80 km/h schnell fahren. Zunächst wird das Auto extrem vereinfacht modelliert. Der Motor als Aktor bekommt als Eingangsgröße eine Soll-Kraft Fsoll. Sein Ausgang ist eine Kraft FM. Er zeigt P-Verhalten mit HM = KPM = 100. Die Übertragungsfunktion des Motors lautet:
Als Strecke wirkt die Kraft über physikalische Gleichungen auf die Geschwindigkeit. Es gilt
F = m ∙ a
und
v(t) = + v0
Wir setzen als Masse m = 1 T an. Insgesamt gilt am Motor
Die Strecke hat offenbar I-Verhalten mit KI = 1 / m. Im Frequenzbereich modellieren wir den Funktionsblock Strecke mit
Hier wird eine Multiplikation der Konstanten mit dem Term vorgenommen. Im Blockschaltbild wird der Term nie mit anderen Termen verrechnet, da er für das Verständnis des Verhaltens wichtig ist. Dieser Term bekommt immer einen eigenen Block. Das Blockschaltbild der Strecke wird folgendermaßen modelliert:
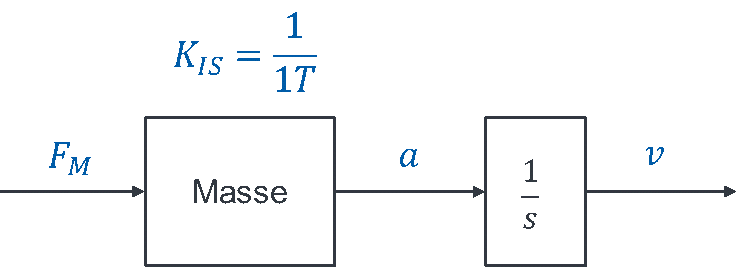
Diese Blöcke bilden das System. Sie werden als System zunächst ohne Regler modelliert.

Sie erkennen, dass hier KPM und KIS zusammengefasst werden könnten. Das ist immer der Fall, wenn Sie P-Verhalten und I-Verhalten hintereinander in Reihe schalten.
Als Regler soll ein P-Regler mit
eingesetzt werden. Das bedeutet, dass Sie im Modell dem Block „Regler“ P-Verhalten mit der Übertragungsfunktion
geben.
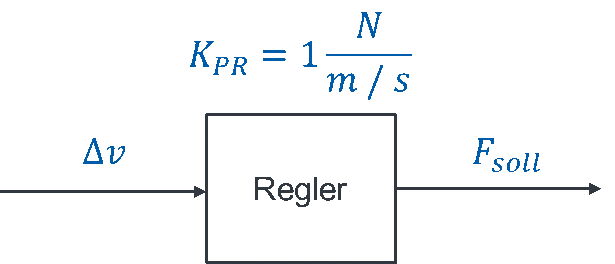
Die Geschwindigkeit wird mit einem Tachometer als Sensor gemessen. Dieser wird nicht modelliert, da seine Übertragungsfunktion HTacho = 1 ist. Das Blockschaltbild des geregelten Systems sieht folgendermaßen aus:

Berechnen wir zunächst A aus den Übertragungsfunktionen der Funktionsblöcke. Es gilt
Hier tritt der Fall auf, dass Sekunde s und komplexe Frequenz s in einem Ausdruck zusammen auftauchen. Achten Sie bei Ihren Rechnungen darauf, diese irgendwie zu unterscheiden.
Mit diesem Wert von A können wir jetzt Führungsverhalten und Störunterdrückung ausrechnen. Wir nutzen hier eine Vereinfachung, die bei komplexen Ausdrücken für A immer genutzt werden kann. Es gilt beim Führungsverhalten
In dieser Form muss er meistens nicht weiter umgeformt werden, um ihn bei s = 0 interpretieren zu können. Setzen wir also
In die Formel ein, dann ergibt sich das Führungsverhalten zu
Im eingeschwungenen Zustand bei s = 0 gilt also HFü = 1 und damit y = w bei d = 0. Damit ist an einem Beispiel gezeigt worden,
1. wie Blöcke mit P-Verhalten und I-Verhalten zusammengefasst werden können
2. wie das Führungsverhalten mit einer umgestellten Formel einfacher analysiert werden kann
3. dass Systeme mit I-Verhalten im A in Systemen ohne Störung keine bleibende Regelabweichung aufweisen.
Weiter