Wichtiger Hinweis: Die Ergebnisse dieses Kapitels sind nur in Systemen ohne Störungen anzuwenden. In späteren Kapiteln werden diese Ergebnisse für Systeme mit Störungen erweitert. Es werden dann andere Formeln als in diesem Kapitel verwendet. Die folgenden Formeln sind also nur gültig, wenn in einem System keine Störung vorliegt.
Im vorletzten Kapitel haben wir die Ähnlichkeit aller proportionalen Systeme zu einer allgemeinen mathematischen Beschreibung dieser Verhaltensweise genutzt. Wir setzen jetzt für unterschiedliche Systeme nur noch andere Werte für kP ein und erhalten damit das spezielle Verhalten unseres Systems.
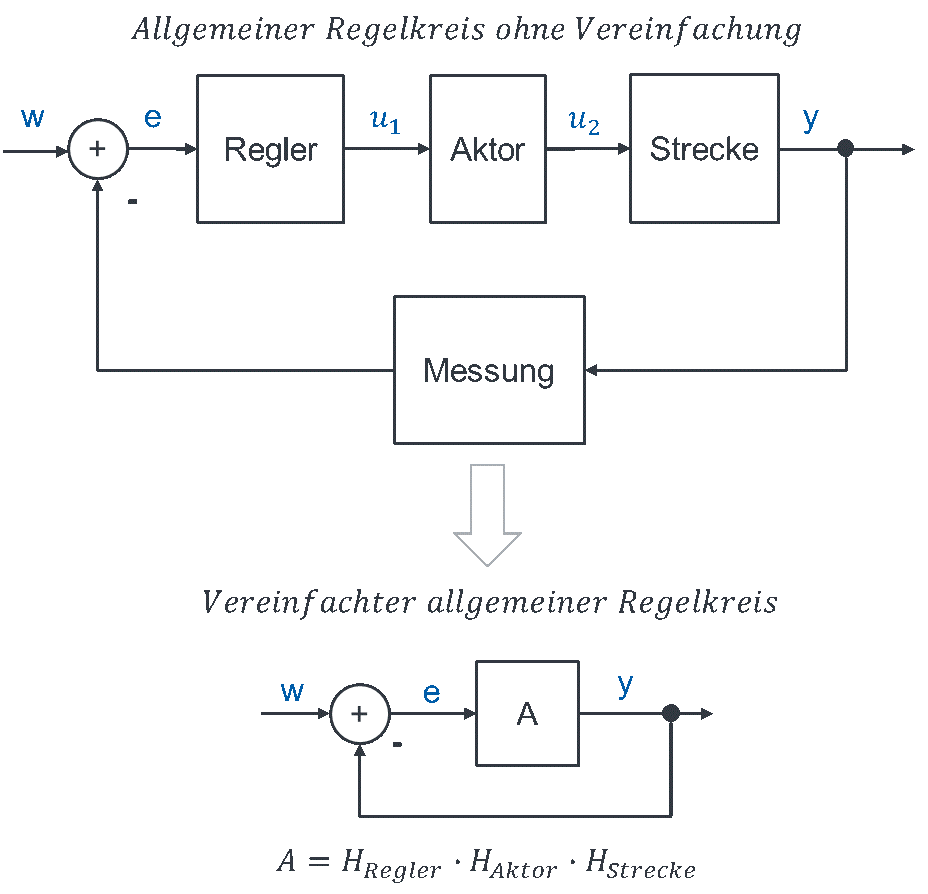
Dieses Verfahren der Ausnutzung von Ähnlichkeit wenden wir jetzt für alle Regelkreise an. Betrachten wir zunächst noch einmal einen allgemeinen Regelkreis. Im allgemeinen Regelkreis werden Funktionsblöcke und Signale allgemein bezeichnet, ohne auf eine konkrete Regelung einzugehen:
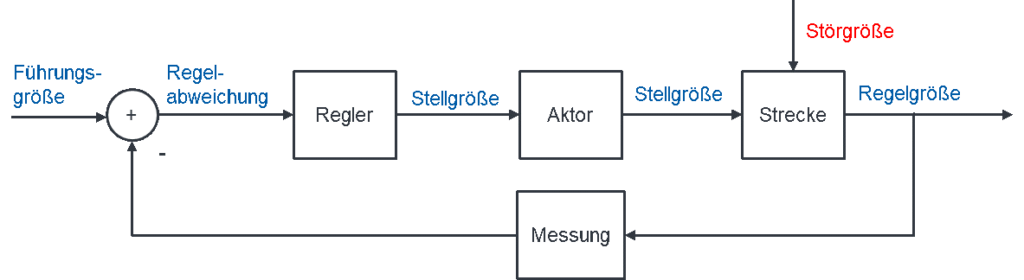
Um zu einer einheitlichen, allgemeinen Lösung für alle möglichen Regelkreise zu gelangen, wird der allgemeine Regelkreis zunächst radikal vereinfacht.
Vereinfachung der Messung
Zunächst gehen wir von einer idealen Messtechnik für die Messung der Regelgröße aus. Diese wandelt die physikalische Größe am Ausgang des Systems ideal und fehlerfrei in eine digitale Zahl um. Die digitale Zahl wird in der Software des Reglers verwendet. Die Übertragungsfunktion der Messung lautet also H = 1. Es wird z. B. beim Tempomaten nur die Größe „analoge Geschwindigkeit“ in die Größe „digitale Geschwindigkeit“ umgewandelt.
Was bedeutet H = 1? Die Ausgangsgröße ist dann gleich der Eingangsgröße. Wenn die Übertragungsfunktion = 1 ist, dann können wir den Block auch weglassen, denn mit H = 1 hat der Block keinen Einfluss auf den Regelkreis. Wir verbinden im stark vereinfachten allgemeinen Regelkreis den Ausgang des Systems also direkt mit dem Subtrahier-Element.
Regler, Aktor und Strecke
Die Funktionsblöcke Regler, Aktor und Strecke sind hintereinandergeschaltet. Die Übertragungsfunktionen hintereinandergeschalteter Funktionsblöcke kann zur Vereinfachung der Struktur durch Multiplikation der Übertragungsfunktionen zu einer Gesamt-Übertragungsfunktion zusammengefasst werden. Es gilt:
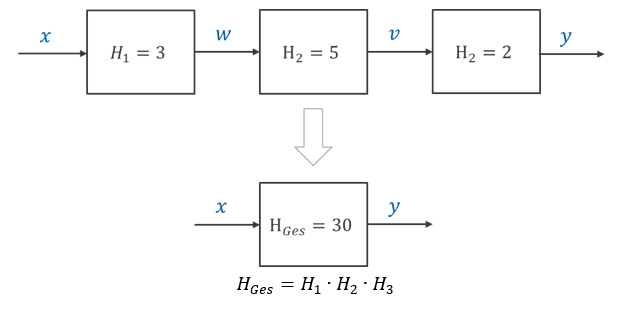
Die Funktionsblöcke „Regler“, „Aktor“ und „Strecke“ im allgemeinen Regelkreis werden zu einem einzigen Funktionsblock zusammengefasst. Den resultierenden Bock benennen wir mit dem Bezeichner „A“. Wir können dann in der allgemeinen Lösung mit einem Parameter A rechnen. Wir weisen A erst später ein konkretes Verhalten eines Systems zu.
Der zusammengefasste Block A besteht also aus dem Regler, dessen Verhalten wir beeinflussen können, sowie Aktor und Strecke, deren Verhalten wir nicht beeinflussen können. Über den Regler haben wir später die Möglichkeit, das Verhalten von A zu beeinflussen.
Der vereinfachte allgemeine Regelkreis sieht folgendermaßen aus: