Bei P-Verhalten ist die Übertragungsfunktion eine Konstante. Allgemein können Übertragungsfunktionen zeitabhängig sein. Bei konstantem Eingang ändert sich dann der Ausgang eines Systems mit der Zeit t. Dies erkennen wir daran, dass das t der Zeit in der Formel von H auftaucht.
Die Zeitabhängigkeit wird mit Hilfe der Sprungantwort vermessen und charakterisiert. Dafür wird am Eingang des Systems ein Sprung in der Eingangsgröße von 0 auf einen konstanten Wert (z. B. Eingang = 1) angelegt. Beim Getriebe wird die Drehzahl N1 von 0 Umdrehungen pro Minute (Einheit rpm wie Rotations per minute) auf 1rpm sprungförmig geändert. Angenommen die Übertragungsfunktion des Getriebes hätte den Wert H = 10, dann würde sich die Ausgangs-Achse 10 Mal so schnell drehen wie die Eingangs-Achse. Die Ausgangsachse würde damit von N2 = 0 rpm auf N2 = 10rpm springen.
Proportionale Systeme reagieren am Ausgang direkt auf Änderungen am Eingang. Es gibt keine zeitliche Verschiebung oder Verzögerung. Bei einem Sprung zum Zeitpunkt t = 1s sieht die Sprungantwort dieses Getriebes mit (angenommenen) H = 10 folgendermaßen aus:
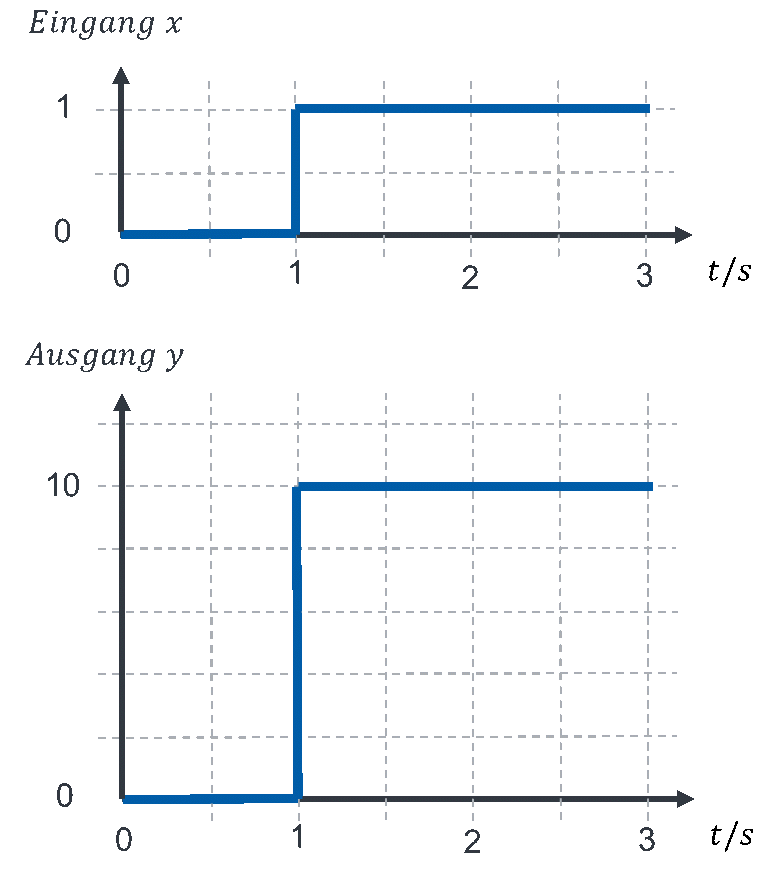
Der Sinn der Sprungantwort erschließt sich erst bei anderen Verhaltensweisen, die zeitabhängig sind. Ich führe die Sprungantwort hier an einem einfachen Beispiel ein.
Nutzen der Sprungantwort
Bei P-Verhalten haben wir ein Wertepaar genommen und damit den charakteristischen Parameter bestimmt. Wenn die Übertragungsfunktion zeitabhängig ist, dann geht das nicht mehr. Wir nutzen deshalb immer die Sprungantwort, um die Verhaltensweise eines Funktionsblocks zu ermitteln und dessen charakteristische Parameter zu ermitteln. Bisher haben wir bei P-Verhalten nur den Parameter kP kennengelernt. Auch diesen können wir aus der Sprungantwort ermitteln.
Mit der Sprungantwort ermitteln wir die charakteristischen Parameter ohne Kenntnis des inneren Aufbaus nur über eine Messung der äußeren Größen. Das ist großartig, denn damit können wir perspektivisch Systeme regeln ohne sie zu verstehen. Das ist insbesondere bei komplexen Systemen wie z. B. einem Auto hilfreich. Als Beispiel nehmen wir einen Hebel, dessen Armlängen wir nicht kennen und auch nicht messen können (oder wollen).
Wir lenken den Eingang des Systems (die Höhe h1) sprunghaft von 0cm auf 1cm aus. Dann messen wir, wie sich der Ausgang verhält. Wenn er von der Auslenkung 0 aus ohne Verzögerung auf einen konstanten Ausgangswert springt, dann verhält sich das System proportional. Wir brauchen zur Charakterisierung des Systems dann noch den Wert kp. Diesen ermitteln Sie aus dem Quotienten von Ausgangswert und Eingangswert. Wenn sich der Ausgangswert z. B. um 10cm ändert, dann können Sie den Proportionalitätsbeiwert folgendermaßen berechnen:
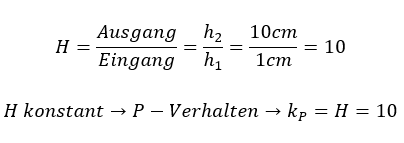
Sie können die Verhaltensweise eines Autos und dessen charakteristische Parameter ermitteln, indem Sie seine Eingangsgröße Gaspedalstellung sprungförmig von 0 auf Vollgas ändern. Dann messen Sie über der Zeit die Ausgangsgröße Geschwindigkeit. Damit können Sie viel über das Verhalten des Autos in einem Regelkreis lernen, ohne dass Sie den Motor oder das Getriebe verstehen müssen. Ich finde das genial.
Sprunghöhe
Die Höhe des Sprungs am Eingang ist beliebig. Warum springen wir mit dem Eingang immer von 0 auf 1? Das hat etwas mit der Übertragungsfunktion zu tun.
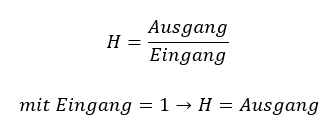
Wenn der Eingang gleich 1 ist, entspricht der Ausgang direkt der Übertragungsfunktion H. Wir sparen einen Rechenschritt. Wenn wir also das Zeitverhalten des Ausgangs bei einem Sprung von 0 auf 1 betrachten, dann sehen wir im Ausgang direkt das Zeitverhalten der Übertragungsfunktion.
Wenn ein Sprung von 0 auf 1 nicht möglich ist, können Sie auf jeden anderen Wert springen. Wenn Sie z. B. von 0 auf 2 springen, dann müssen Sie den Ausgang durch 2 teilen und haben dann die Übertragungsfunktion. Das ergibt sich direkt aus der Formel zwischen Eingang, Ausgang und Übertragungsfunktion.
Weiter