Genau wie in Grundlagen der Elektrotechnik nutzen wir auch in der Regelungstechnik die LaPlace-Transformation, um Funktionsblöcke mathematisch einfacher beschreiben zu können. Beim I-Verhalten im letzten Kapitel kam bereits eine Integration vor. Bei weiteren Verhaltensweisen wird es mathematisch nicht schöner. Die LaPlace-Transformation bietet folgende hilfreiche Vorteile:
1. Eine Integration im Zeitbereich wird zu einem Produkt mit 1/jω im Frequenzbereich
2. Eine Ableitung im Zeitbereich wird zu einem Produkt mit jω im Frequenzbereich
Komplexe Frequenz
Regelungstechniker verwenden einen etwas andere Frequenz-Parameter als Elektrotechniker. Sie Kreisfrequenz ω aus der Elektrotechnik wird erweitert. Die komplexe Frequenz ist allgemein folgendermaßen definiert:

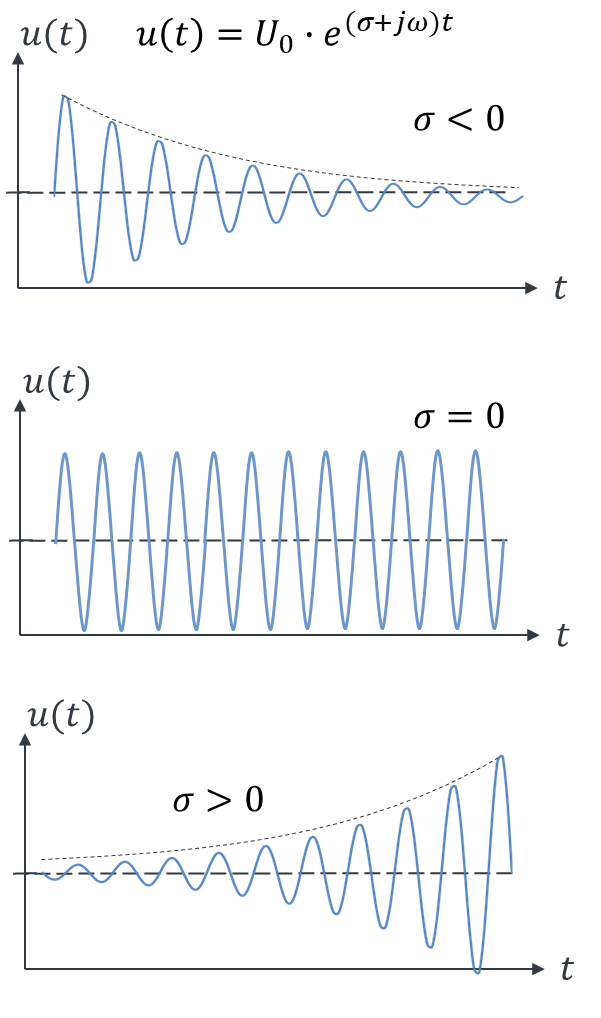
In der Elektrotechnik haben wir bisher nur dauerhafte sinusförmige Schwingungen betrachtet. Dauerhafte ungedämpfte Schwingungen, deren Spitzenwert über der Zeit unveränderlich ist, werden auch immer mit s = jω mit σ = 0 berechnet. Deshalb nutzen die faulen E-Techniker in der Wechselstromrechnung nur den Teil s = jω. Der Parameter σ definiert die Dämpfung einer sinusförmigen Schwingung. Wenn der Spitzenwert einer Sinus-Schwigung über der Zeit z. B. immer weiter abnimmt, dann ist ein σ im Spiel.
Betrachten Sie z. B. die Schwingung einer Schaukel, die Sie loslassen. Die Schaukel schwingt mit der Frequenz jω hin und her. Sie wird aber auch langsamer und irgendwann steht sie still. Gründe dafür sind Reibung und Luftwiderstand. Bremsen führt zu einer Dämpfung der Schwingung. Für σ < 0 wird eine Schwingung gedämpf. Bei σ = 0 ist sie ungedämpft und ändert sich nicht über der Zeit. Bei σ > 0 wird die Schwingung sogar verstärkt, ihre Amplitude steigt also immer weiter an. Das passiert, wenn Sie die Schaukel im richtigen Moment regelmäßig anschubsen. Das betrachten wir hier aber nicht weiter.
In diesem Tutorial betrachten wir erst später gedämpfte Systeme, deshalb können Sie σ zunächst ignorieren. In der Regelungstechnik verwenden wir die komplexe Frequenz s immer dann, wenn wir in der Elektrotechnik jω verwenden. Das hat Tradition, und damit werden Sie im Alltag konfrontiert werden. Deshalb bringe ich s bereits jetzt. Mathematisch ersetzen wir also in den Gleichungen jω immer durch s.
Die Beschreibung mit s ist auf den ersten Blick deutlich einfacher als die mit jω, weil keine komplexen Zahlen mehr in den Rechnungen auftauchen. Die komplexen Zahlen sind aber nur versteckt, denn natürlich ist s komplex. Die Rechnungen wirken in der Regelungstechnik aber quasi reell und die komplexen Zahlen bleiben in s „gekapselt“.

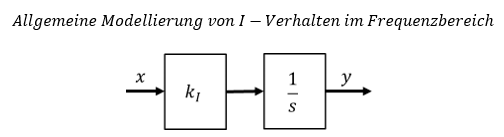
I-Verhalten als Zeitfunktion wird durch eine Integralgleichung beschrieben. Es ist mathematisch viel einfacher, wenn wir im Frequenzbereich mit s rechnen. I-Verhalten ist dann nur noch eine Multiplikation mit dem Faktor kI / s.
Üblicherweise teilen wir die Faktoren bei der Integration in zwei Blöcke auf. Der Faktor kI alleine weist P-Verhalten auf. Der Faktor 1/s zeigt an, dass hier I-Verhalten vorliegt.
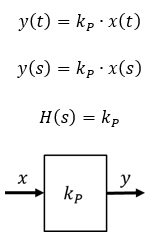
Auch P-Verhalten kann im Frequenzbereich mit einer komplexen Übertragungsfunktion abgebildet werden. Diese ist zum Glück genau wie im Zeitbereich, denn es gilt für P-Verhalten:
Wichtige Ergänzung: Der Buchstabe „s“ wird bereits für Sekunden verwendet. Wenn reale Systeme geregelt werden, kommen in den Formeln sowohl Sekunden als auch s als komplexe Frequenz vor. Um eine Verwechslung zu vermeiden, wird die Sekunde in solchen Fällen immer als s fett dargestellt, die komplexe Frequenz s nicht.
Video zum Sinn von Transformationen
Weiter