Der Regler steuert den Aktor an. Der Aktor wirkt auf die Strecke. Dies ist der gewollte Weg, wie das System beeinflusst wird. Alle anderen äußeren Einflussgrößen, die auf die Regelgröße wirken, bezeichnen wir als Störungen. Das ist unabhängig davon, ob sie im Wortsinn „stören“, oder ob sie eine normale Funktion im System ausüben.
Ein Ziel der Regelungstechnik lautet, dass die Regelgröße der Führungsgröße entsprechen soll. Das gilt auch, wenn Störungen auf die Regelgröße wirken. Alle bisherigen Ziele der Regelungstechnik gelten auch bei Störungen.
Störungen werden als Eingangsgrößen modelliert. Sie können an unterschiedlichen Stellen im Regelkreis wirken. Für die Auswirkung einer Störung im System ist es entscheidend, an welcher Position im Regelkreis eine Störung auftritt. Betrachten wir zum Einstieg zwei Beispiele für Störungen:
Beispiel 1: Eimer
Ein mit Wasser gefüllter Eimer weist einen Zulauf und einen Ablauf auf. Der Zulauf ist die Eingangsgröße. Der Aktor ist das Ventil, das den Zulauf steuert. Wir wollen den Füllstand des Eimers regeln, deshalb ist der Füllstand die Regelgröße. Der „normale“ Weg der Regelung stellt den Füllstand über Regler und Aktor, also über den Zulauf. Die Strecke ist der Eimer selbst.
Der Ablauf wirkt genauso wie der Zulauf auf den Füllstand. Er wird aber nicht über den Aktor des Reglers gesteuert, deshalb wird er als Störung definiert. Wird Wasser abgelassen, muss über den Zulauf Wasser nachgefüllt werden. Die Menge an Wasser, die insgesamt den Füllstand ändert, ist die Differenz zwischen Zulauf und Ablauf. Für Zu- und Ablauf gilt

Für die Modellierung hangeln wir uns an der Formel entlang. Zu- und Ablauf werden zuerst subtrahiert und dann wird das Ergebnis integriert. Im Blockschaltbild wirkt die Störung Ablauf „links“ vom Integral. Der Ablauf wird vom Zulauf subtrahiert. Das Blockschaltbild aus Regler, Aktor, Störung und Strecke sieht folgendermaßen aus:
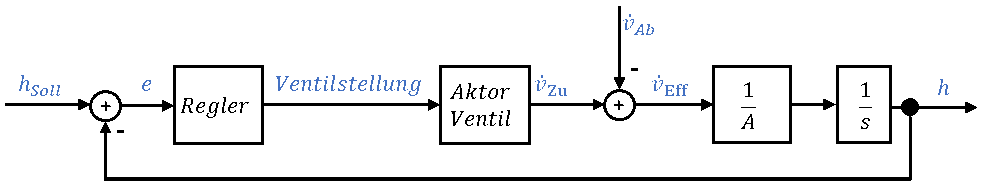
Die Mathematik stellt erstmal nur den rechten Teil des Blockschaltbilds dar, also den Teil zwischen Aktor und Regelgröße. Wir schließen den Regelkreis mathematisch nach dem nächsten Beispiel.
Beispiel 2: Tempomat
Bei der Geschwindigkeitsregelung des Autos ist der Motor der Aktor und das Fahrzeug die Strecke. Störungen sind z. B. Fahrtwind und Steigung der Fahrbahn. Sie wirken als Kraft auf das Fahrzeug. Allgemein gilt folgender Zusammenhang zwischen Kraft und Geschwindigkeit:
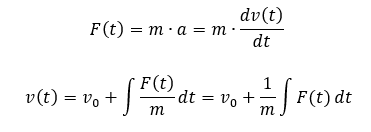
Die Geschwindigkeit ist also über ein Integral mit der Kraft verknüpft. Wenn wir das im Frequenzbereich berechnen, gilt
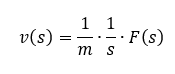
Auf die Geschwindigkeit wirken mehrere Kräfte. Zunächst wirkt die Kraft des Motors als Ausgang des Aktors auf die Geschwindigkeit in Fahrtrichtung. Wenn das Auto eine Steigung hochfährt, dann wirkt eine Bremskraft entgegen der Fahrtrichtung. Auch der Fahrtwind oder Reibung wirken bremsend, also als Kräfte entgegen der Kraftrichtung des Motors. Das können wir als Summe berechnen. Die Summanden der Störgrößen werden addiert, sie sind aber negative Zahlen, so dass sie entgegen der Richtung des Motors wirken.

Setzen wir die Kraftgleichung in die Geschwindigkeitsgleichung ein. Die Kräfte werden erst addiert zu einer Gesamtkraft, und diese wird dann integriert. Deshalb wird die Kraftsumme im Blockschaltbild links von der Integration modelliert.
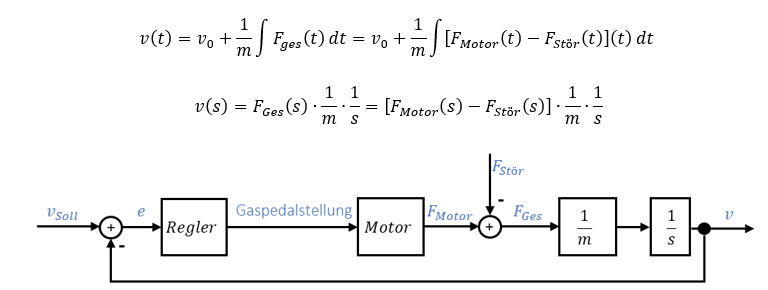
Im Modell werden – wie in den Gleichungen – zuerst die Kräfte subtrahiert und dann wird integriert. Sie erkennen, dass die Modellierung beider Systeme ähnlich ist, obwohl sie völlig unterschiedliche Funktionen haben. Betrachten wir als nächstes, wie Störungen in geregelten Systemen berechnet werden.
Weiter