Ein System schwingt, wenn sich sein Ausgang über der Zeit sinusförmig verändert. Ein Beispiel ist die Schaukel. Wird die Schaukel nicht angestoßen, schwingt sie auch nicht. Wird sie angestoßen (Eingangssprung), beginnt sie hin und her zu schwingen. Sie schwingt weiter, wenn man sie nicht weiter anschubst (Eingang = 0). Ein sinusförmiger Verlauf ist typisch für schwingendes Verhalten. Schwingen ist in der Regelungstechnik i. A. nicht gewollt. Wenn Sie einen Tempomaten im Auto betreiben, dann wollen Sie nicht, dass die Geschwindigkeit des Autos schwingt, sie soll konstant sein.
Bei gewolltem Schwingen (wie an der Schaukel) stimulieren wir das System am Eingang über einen Impuls so, dass es schwingt. Dafür müssen wir es zum richtigen Zeitpunkt in die richtige Richtung stimulieren. Wenn ein System aus der Ruhelage heraus angestoßen wird, dann erkennen wir am sinusförmigen Zeitverlauf der Ausgangsgröße, ob es schwingt. In der Regelungstechnik regen wir so ein System mit einem Sprung im Eingang an und messen dessen Sprungantwort. Die Sprungantwort beschreibt, wie sich die Schaukel nach einem Anstoßen aus der Ruhelage heraus bewegt.
Mathematik von Schwingungen
Mathematisch schwingt ein System mit der Kreisfrequenz ω0, wenn seine Übertragungsfunktion folgendes Verhalten aufweist:
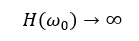
Das gilt, wenn der Nenner im Bruch der Übertragungsfunktion zu 0 wird. Das ist i. A. nur bei einer bestimmten Frequenz der Fall. Eine Schaukel schwingt auch mit einer festen Frequenz. Wir nennen diese Frequenz die Resonanzfrequenz eines Systems. Die Übertragungsfunktion einer Schaukel wird bei der Resonanzfrequenz ebenfalls unendlich groß.
Betrachten wir ein gegengekoppeltes System aus zwei hintereinander geschalteten I-Blöcken in einem Regelkreis. Es sind zwei Speicher im Spiel, also ist eine Schwingung möglich. Berechnen wir zunächst A und dann das Führungsverhalten:

Die Sprungantwort eines schwingenden Systems schwingt im Anschluss an den Eingangssprung. Der Zeitverlauf der Sprungantwort des Beispielsystems mit k = 1 ist in der unteren Abbildung dargestellt. Der Sprung der Eingangsgröße in blau erfolgt bei t = 1s.
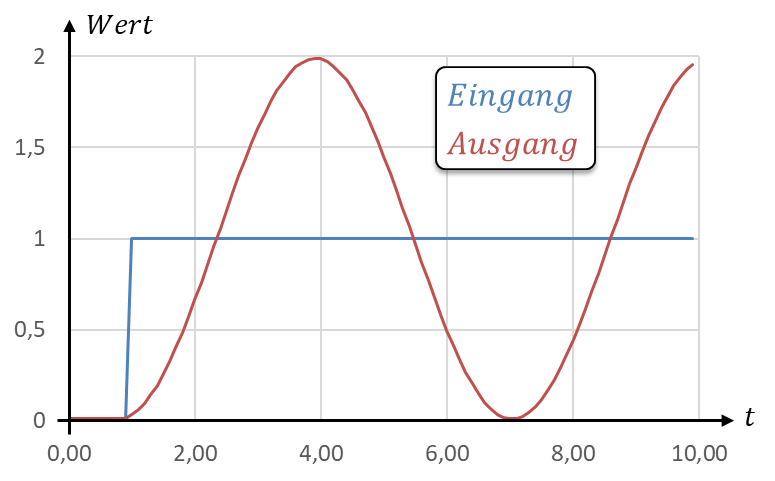
Die Schwingung der Ausgangsgröße startet, sobald der Eingang springt. Die Periodendauer T0 in der Grafik entspricht dem berechneten Wert von T0 = 6,28s. Sie kann aus dem Abstand der Maxima bestimmt werden. Eine sinusförmige Dauer-Schwingung wird über den Parameter „Schwingfrequenz“ oder „Resonanzfrequenz“ charakterisiert. Dieser Parameter liegt immer als Kreisfrequenz ω, als Frequenz f und als Periodendauer T vor.
Der Spitzenwert der Schwingung beträgt 1. Die Ausgangsgröße schwingt nach dem Sprung um die Eingangsgröße w = 1 herum.
Aufgabe
Modellieren Sie das geregelte System in Matlab Simulink. Regen Sie das System mit einem Sprung von 0 auf 1 an. Variieren Sie kI und beobachten Sie, wie sich das Ausgangsverhalten ändert. Hier die Lösung für kI = 1:
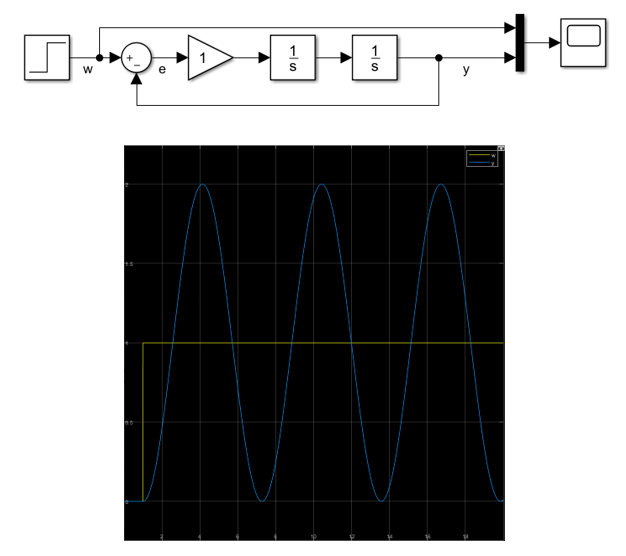
Es gibt Systeme mit PT-2-Verhalten, die nicht schwingen können. Andere können nur bei bestimmter Parametrierung schwingen. Wieder andere schwingen immer, egal wie sie parametriert wird. Dies hängt von der „Dämpfung“ eines Systems ab. Eine Schaukel wird z. B. durch Reibung gedämpft. Eine ungedämpfte Schwingung schwingt mit konstantem Spitzenwert unendlich lange weiter.
In der Regelungstechnik wird die Dämpfung mit dem Buchstaben „D“ bezeichnet. Es werden folgende Fälle unterschieden:
D = 0: Kontinuierliche ungedämpfte Schwingung
0 < D < 1: Abklingende Schwingung
D = 1: Aperiodischer Grenzfall: Gerade so keine Schwingung
D > 1: Nicht schwingendes System
Allgemein gilt folgende Übertragungsfunktion für Systeme mit PT-2-Verhalten:
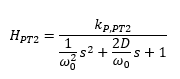
Die Dämpfung D erkennen wir immer im Vorfaktor von „s“ im Nenner der Übertragungsfunktion. Im Beispiel des Regelkreises weiter oben gilt:
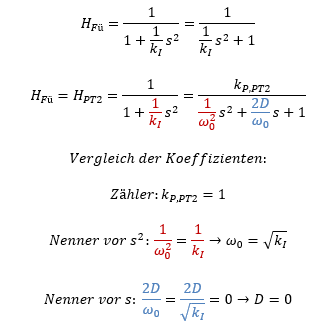
Durch den Koeffizientenvergleich können wir die Resonanz-Kreisfrequenz ω0 auf eine allgemeinere Weise bestimmen als aus dem ersten Ansatz weiter oben im Text. Dafür vergleichen wir einige Faktoren im Führungsverhalten und in der allgemeinen Übertragungsfunktion von PT-2-Verhalten. Der hier beschriebene Ansatz funktioniert allgemein bei allen Systemen mit PT-2-Verhalten.
Weil das Führungsverhalten im Nenner keinen Term mit s enthält, ist dessen Vorfaktor offenbar gleich 0. Das bedeutet, dass hier D = 0 gelten muss. Das ist die mathematische Bedingung für eine ungedämpfte Schwingung mit konstantem Spitzenwert.
Weiter