Viele geregelte Systeme (alle hier betrachteten Systeme) sind sich in ihrer Struktur ähnlich. Die Verhaltensweise von Teilsystemen und Funktionsblöcken kann mit P-Verhalten, I-Verhalten oder anderen Verhaltensweisen charakterisiert werde. Um zu einer einheitlichen, allgemeinen Lösung für alle möglichen Regelkreise zu gelangen, wird der Regelkreis zunächst radikal vereinfacht.
Vereinfachung der Messung
In der Regelungstechnik gehen wir zu Vereinfachung von einer idealen Messtechnik für die Messung der Regelgröße aus. Diese wandelt die physikalische Größe am Ausgang des Systems ideal und fehlerfrei in eine digitale Zahl um. Die digitale Zahl wird in der Software des Reglers verwendet. Die Übertragungsfunktion der Messung ist also H = 1. Es wird beim Tempomaten nur die Größe „analoge Geschwindigkeit“ in die Größe „digitale Geschwindigkeit“ umgewandelt. Wenn die Übertragungsfunktion = 1 ist, dann können wir den Block auch weglassen, denn mit H = 1 hat der Block keinen Einfluss auf den Regelkreis. Wir verbinden im stark vereinfachten allgemeinen Regelkreis den Ausgang des Systems also direkt mit dem Subtrahier-Element.
Regler, Aktor und Strecke
Im einfachsten Fall weisen Regler, Aktor und Strecke alle P-Verhalten auf. Die Eingangsgröße des Reglers – die Regelabweichung – wird also drei Mal in Folge mit einem Faktor multipliziert. Dies kann zu einer Multiplikation mit einem einzigen Faktor vereinfacht werden, in dem das Produkt aller Faktoren zusammengefasst wird. Alle drei Funktionsblöcke werden also zu einem einzigen Funktionsblock mit der Bezeichnung „A“ zusammengefasst. Wir können A später wieder kompliziertere Verhaltensweisen zuordnen. Der zusammengefasste Block A besteht also aus dem Regler, dessen Verhalten wir beeinflussen können, sowie Aktor und Strecke, deren Verhalten wir nicht beeinflussen können. Über den Regler haben wir also die Möglichkeit, das Verhalten von A zu beeinflussen.
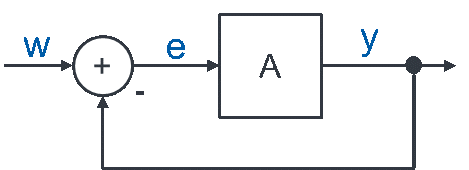
Der vereinfachte allgemeine Regelkreis sieht folgendermaßen aus: