Es gibt ein allgemeines Vorgehen, wenn Sie mit der Mathematik nicht weiterkommen: Die Transformation. Eine Transformation überführt ein Problem in eine andere „Art“ von Mathematik.
Mit der Laplace-Transformation gelingt es, die Mathematik so stark zu vereinfachen, dass Netzwerke mit Wechselgrößen mit ähnlich geringem mathematischem Aufwand wie für Gleichgrößen berechnet werden können. Diese Art der Mathematik benötigen Sie im weiteren Studienverlauf in der Messtechnik, der Regelungstechnik, der Energietechnik, bei digitalen Filtern und in vielen weiteren Disziplinen. Es macht Sinn, dieses Kapitel jetzt richtig zu verstehen.
Die allgemeine Formel der LaPlace-Transformation lautet:

Die LaPlace-Transformation selbst ist mathematisch nicht schön. Wir müssen aber zum Glück immer nur eine Funktion transformieren, denn wir rechnen bei Wechselspannung ja immer mit der Sinus-Funktion. Und diese eine Lösung steht oben in der untersten Gleichung. Damit sind wir – was die Transformationsmathematik mit dem Integral betrifft – bereits feritg.
Alle Wechselgrößen (Wechselspannung, Wechselstrom, Wechselleistung) bestehen immer aus Spitzenwert, Sinus, Kreisfrequenz, Zeit und Phasenwinkel. Für das Beispiel einer Wechselspannung haben wir folgende Parameter:
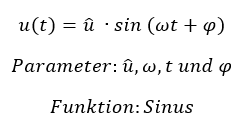
Die LaPlace-Transformation für diese Funktion ist bekannt. Wir können also einfach das Ergebnis nehmen und damit arbeiten.
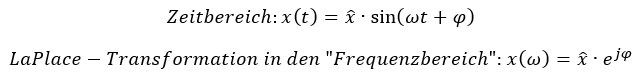
Wir brauchen für die LaPlace-Transformation nur zwei der drei Parameter einer Wechselgröße: Den Spitzenwert und die Phasenverschiebung. Bei der Laplace-Transformation wird die Menge an Information über das Signal massiv reduziert. Im Zeitbereich werden alle 4 Parameter der Wechselgröße berücksichtigt.
Betrachten wir zwei Beispiele:

Jetzt müssen wir noch klären, was „Frequenzbereich“ bedeutet, was das „j“ in den Formeln soll und wie man mit diesen Exponentialfunktionen rechnen. Ich kann Ihnen hier versprechen: Das ist deutlich einfacher als es auf den ersten Blick erscheint.
Weiter