Hinweis: Das Kapitel „Wasserspeicher“ mit seinen drei Unterkapiteln ist nicht prüfungsrelevant. Es dient als Erklärung, wie Integralrechnung anschaulich funktioniert. Wenn Sie das nicht interessiert, dann lesen Sie ab Kapitel „Elektrische Energiespeicher“ weiter. Sie sollten zumindest das Unterkapitel „Grafische Lösung“ lesen, das hilft beim Lösen von Klausuraufgaben zum Thema Speicher.
Wir beginnen die Erklärungen zu Energiespeichern mit Wasserspeichern. Dann übertragen wir die Erkenntnisse auf elektrische Energiespeicher.
Betrachten wir einen Wassereimer als Speicher für Wasser. Er wird über einen Wasserhahn befüllt. In seinem Boden befindet sich ein Ablauf, mit dem er über einen Wasserhahn geleert werden kann. Wie verhält sich die Höhe des Füllstands h des Eimers zum Zu- und Ablauf von Wasser?
Der Füllstand h steigt an, wenn Wasser in den Eimer läuft. Je länger Wasser zuläuft, desto höher ist anschließend der Füllstand h. Je mehr Wasser pro Zeit zuläuft, desto schneller steigt der Füllstand h an. Wird der Zulauf gestoppt, behält der Eimer den aktuellen Füllstand bei.
Wird mit der gleichen Wassermenge statt dem Eimer ein Schwimmbad befüllt, dann steigt der Füllstand deutlich langsamer, es liegt also eine Abhängigkeit von der Grundfläche A vor.
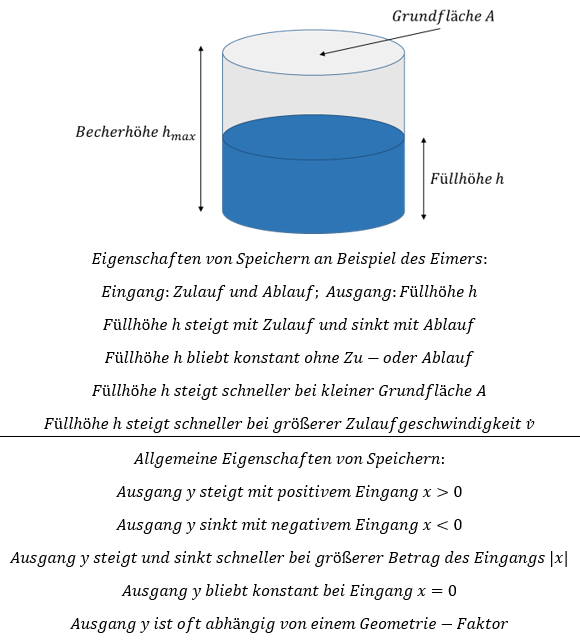
Dieses oben beschriebene Verhalten wird mathematisch mit einem Integral beschrieben. Es gilt für einen Füllvorgang zwischen den Zeiten tStart und tEnde mit dem Zufluss an Wasser:

Die Grundfläche A des Eimers ändert sich nicht. Sie ist über der Zeit konstant. Sie wird deshalb vor das Integral gezogen.
Die Formel beschreibt den Füllstand des Wassers h zum Zeitpunkt tEnde. Er hängt vom Füllstand vor der Befüllung h0 ab, der zum Zeitpunkt tStart vorliegt, also kurz bevor der erste Wassertropfen den Eimer erreicht. Dies ist in der allgemeinen Mathematik der Parameter c in
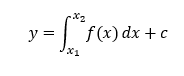
Der Füllstand ergibt sich anschaulich aus der vollständigen Vergangenheit des Befüllens und Leerens des Eimers. Die Summe des gesamten Zulaufs minus der Summe des gesamten Ablaufs ergibt den aktuellen Füllstand. Den vorherigen Füllstand h0(tStart) benötigen wir nur, wenn wir die Vergangenheit aus Faulheit abschneiden und sie als Startwert einer neuen Betrachtung einfrieren.
Die Änderung während des Füllvorgangs wird über das Integral beschrieben. Es wird über der Zeit t integriert, nicht mehr über dem allgemeinen Parameter x. Beim Rechnen mit realen Größen müssen Einheiten berücksichtigt werden. Folgende Einheiten gelten im Beispiel oben:
