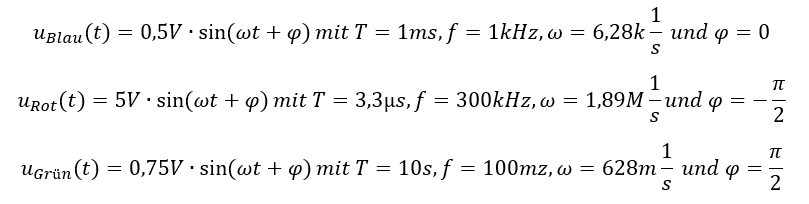Die Wechselspannung an einer Steckdose u(t) kann mit der Sinus-Mathematik aus dem vorherigen Kapitel beschrieben werden. Die Formel aus Zahlen b(t) wird im nächsten Schritt auf eine Spannung u(t) mit Einheiten übertragen. Dafür wird die Gleichung mit einer Spannung multipliziert.
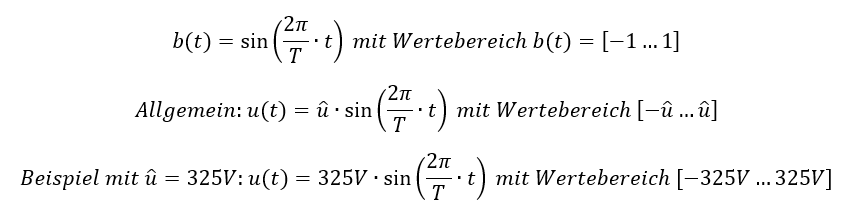
Der Vorfaktor gibt dem allgemeinen Sinus eine technische Bedeutung. Ein Spannungsverlauf bekommt einen Vorfaktor vor den Sinus, der den Maximalwert der Spannung und die Einheit Volt beinhaltet. Damit weist der Umfang des Kreises nicht mehr den Wert 1, sondern den Wert 325V auf. Der Spitzenwert (im Beispiel 325V) bestimmt den maximalen und den minimalen Wert der Spannung. Zwischenwerte der Spannung zwischen den Extremwerten können Sie durch Einsetzen von t in die Gleichung errechnen.
Warum nehme ich im Beispiel diesen krummen Wert 325V? Weil das der Spitzenwert der Wechselspannung an einer Steckdose ist.
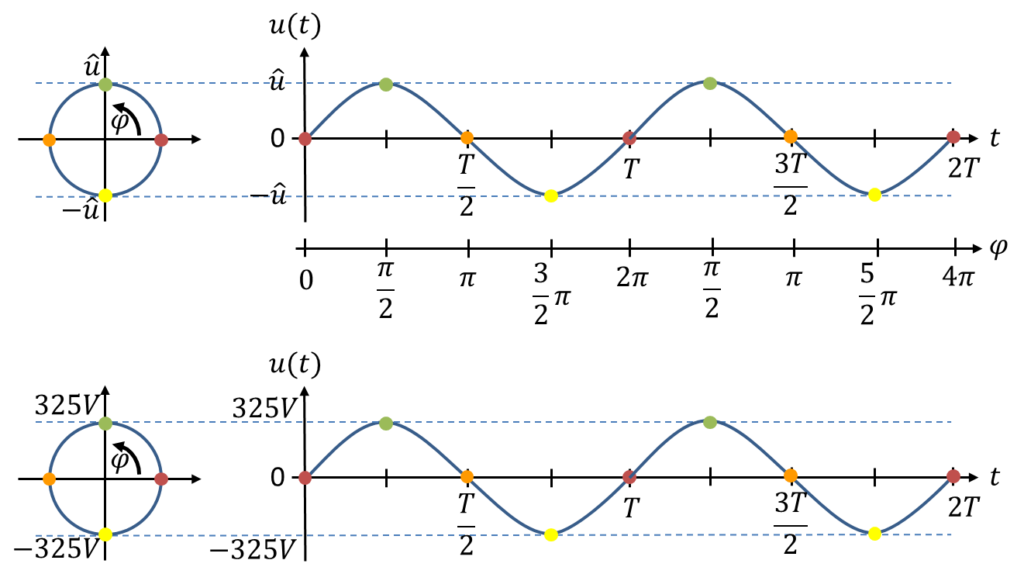
Der zeitliche Verlauf der Spannung ist in der Abbildung oben über zwei Perioden T abgebildet. Eine Wechselspannung hört nicht nach einer Periode auf zu schwingen, sie schwingt i. A. über sehr viele Perioden weiter. Die Spannung an der Steckdose schwingt schon seit mehr als 100 Jahren auf und ab.
Als nächsten Schritt lösen wir uns in der Zeitachse von der Periodendauer T. Wenn Sie Zeitverläufe realer Wechselspannungen messen, dann liegen auf der X-Achse echte Zeitwerte vor. Dafür brauchen wir den Begriff der Frequenz.
Frequenz
Die Frequenz f gibt an, wie oft ein Ereignis pro Zeit geschieht. Nehmen wir aus der Musik den Begriff „Beats per Minute“. Er gibt an, wie viele Bass-Beats pro Minuten in einem Song vorkommen. Je schneller der Song ist, desto mehr Beats kommen pro Minute vor. Dies stellt bereits eine Frequenz dar. 120 Beats per Minute entsprechen 2 Beats pro Sekunde. Die Frequenz wird in der Technik immer auf eine Sekunde bezogen.
In der Wechselstromtechnik wird der Begriff der Frequenz genutzt um zu zählen, wie viele Perioden ein Signal pro Sekunde aufweist. Also wie oft das Signal b(t) den Kreis pro Sekunde umrundet. Die Frequenz wird in der Einheit Hertz (Hz) angegeben. Dies entspricht der SI-Einheit [Hz]=1/s. Die Spannung aus der Steckdose weist die Frequenz f = 50Hz auf. Das bedeutet, dass die Spannung 50 vollständige Perioden des Sinus pro Sekunde durchläuft. Wenn 50 Perioden in eine Sekunde passen, dann dauert eine Periode eine 50stel Sekunde. Die Periodendauer ist mit der Frequenz verknüpft. Es gilt
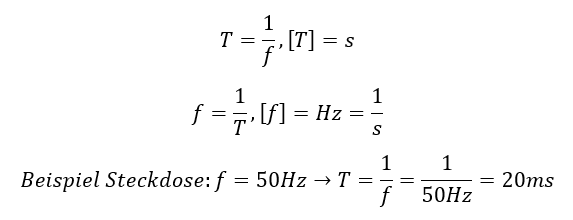
Die Formel passt auch von den Einheiten her, denn die Periodendauer ist eine Zeit, die in Sekunden angegebene wird. Die Frequenz wird in Hertz, also in 1/s angegeben. Die Spannung an der Steckdose mit f = 50Hz zeigt folgenden Zeitverlauf über zwei Perioden:
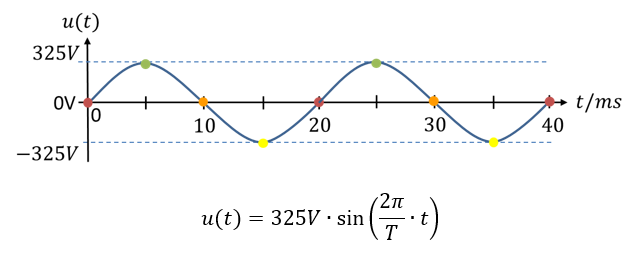
Setzen wir uns gedanklich auf die Sinusfunktion in der oberen Abbildung und lassen die Zeit t verstreichen. Mit der Zeit wandert die Spannung entlang der Funktion zwischen dem minimalen und dem maximalen Spannungswert hin und her. Es gibt für jeden Zeitpunkt t einen zugehörigen Spannungswert u(t), den man entweder grafisch aus der Abbildung ablesen kann oder mathematisch mit der Formel berechnen kann. Dieser momentane Spannungswert wird als Amplitude bezeichnet. Der Betrag der Extremwerte der Kurve entspricht dem Spitzenwert.
Eine Frequenz wird gerne als Tonhöhe veranschaulicht. Ein Lautsprecher besteht aus einer schwingenden Membran, die Luft bewegt. Die Membran wird von einem Elektromagneten oder Piezo bewegt, dessen Auslenkung proportional zur Spannung ist. Damit ist der erzeugte Schall abhängig von der Spannung am Lautsprecher.
Die Intensität des Schalls – also seine Lautstärke – ändert sich mit dem Spitzenwert der Spannung. Die Tonhöhe mit der Frequenz der Spannung. Dazu mehr unter diesem Link.
Kreisfrequenz
Die Kreisfrequenz ω ist weniger anschaulich als die Frequenz f. Sie beschreibt die Anzahl von vollständigen Kreisdurchläufen der Länge 2π pro Sekunden. Es gilt
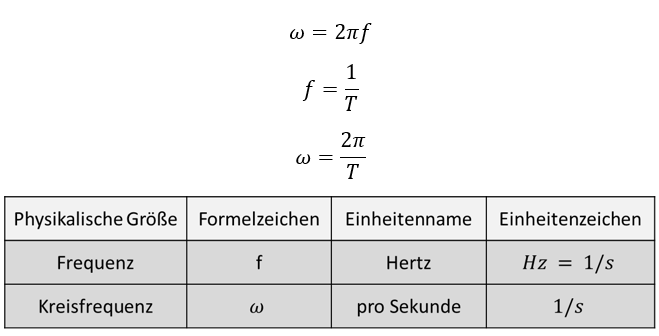
Eigentlich brauchen wir keine weitere Frequenz-Größe. Die Frequenz f wäre ausreichend, um alles in der Elektrotechnik zu beschreiben. Die Kreisfrequenz ω wird dennoch an vielen Stellen in der Praxis genutzt. Sie macht die Formel zur Beschreibung von Wechselgrößen einfacher, denn es entfällt der Term 2π:
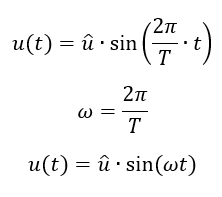
Die Einheit der Kreisfrequenz ist leider nicht Hz sondern [ω] = 1/s. Das ist zwar die gleiche SI-Einheit wie bei der Frequenz f, dennoch müssen (auch in der Klausur) die Kreisfrequenz ω immer in 1/s und die Frequenz f in Hz angegeben werden.
Phasenwinkel
Bisher haben wir angenommen, dass der Verlauf der Spannung zum Zeitpunkt t = 0s auch den Winkel φ = 0 aufweist. Das ist im Allgemeinen nicht der Fall. Es gibt bei einer Zeit keinen echten Nullpunkt. Das wäre vielleicht der Zeitpunkt des Urknalls, aber sicher nicht irgendeine Zeit, zu der eine Sinusspannung beginnt. Wie bei elektrischen Potentialen wird der Bezugspunkt der Zeit von uns frei festgelegt. Bei Spannungen und Potentialen haben wir selbst definiert, welches Potential die Masse als Bezugspunkt aufweist. Mit dieser willkürlichen Festlegung können wir dann rechnen.
Wir können den Nullpunkt oder Bezugspunkt der Zeit frei festlegen. Die Steckdosenspannung durchläuft 50 Perioden pro Sekunde. Bei welcher Zeit t wir mit der mathematischen Beschreibung beginnen ist beliebig. Wir können den Nullpunkt der Zeit also so legen, wie er uns mathematisch am besten passt. Wir können ihn so legen, dass alle Sinusgrößen ohne Verschiebung bei t = 0s mit φ = 0 beginnen.
Wenn zwei sinusförmige Verläufe gleichzeitig vorhanden sind und diese in einer Grafik dargestellt werden, können diese zeitlich gegeneinander verschoben sein. Die Verschiebung ist unabhängig vom gewählten Bezugspunkt immer gleich. Es ist egal, wo wir anfangen die Kurven zu zeichnen, sie sind zueinander verschoben. Eine zeitliche Verschiebung um die Zeit t entspricht einer Änderung um einen Winkel φ am Kreis. Dazu folgendes Beispiel zweier Wechselspannungen mit einem Spitzenwert von jeweils 1V:
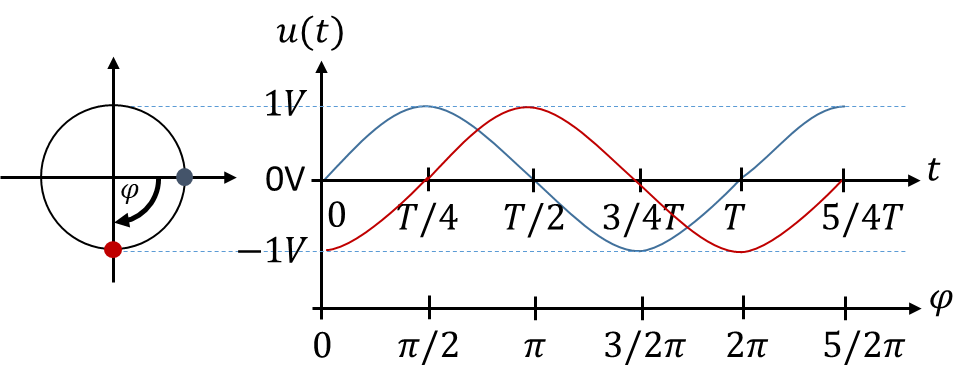
Der rote Spannungsverlauf ist um Δφ = -π/2 gegenüber dem blauen Verlauf nach „rechts“ verschoben. Wir sprechen auch davon, dass die rote Kurve der blauen zeitlich „vorauseilt“. Die blaue eilt der roten Kurve „nach“. Auf der Zeitachse rechts handelt es sich um eine Verschiebung um eine Viertel-Periode in Richtung Zukunft. In der Kreisdarstellung links entspricht dies einer Drehung um 90° oder π/2 im Uhrzeigersinn.
Mathematisch beschreiben wir solche Verschiebungen durch die Ergänzung des Winkels im Argument des Sinus:
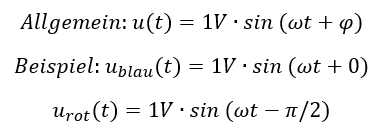
Warum ist der Verschiebungswinkel bei der roten Kurve negativ, wenn die Kurve nach rechts verschoben ist? Intuitiv würden wir einen Winkel addieren. Setzen wir einen Zeitwert in die Formel ein, dessen Ergebnis wir kennen. Das geht mit Zeiten am besten, wenn der Ausdruck ωt wieder durch 2π/T ersetzt wird. Wir prüfen, ob die Formel beim Zeitpunkt t=T/2 den aus der Grafik erwarteten Wert von U=1V annimmt.
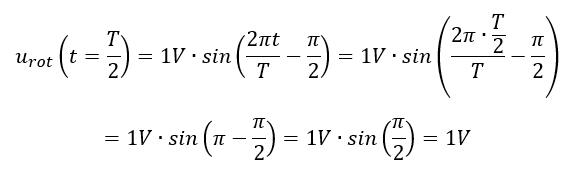
Offenbar bildet die Formel den Verlauf aus der Grafik richtig ab. Wenn der Winkel addiert (statt subtrahiert) wird, dann kommt ein falsches Ergebnis raus. Berechnen Sie das zur Übung mal.
Ist eine Kurve gegenüber dem (beliebig gewählten) Nullpunkt der Zeit nach links verschoben, muss ein positiver Winkel im Argument des Sinus addiert werden. Ist die Kurve in der Zeit nach rechts verschoben, wird ein positiver Winkel subtrahiert. Bitte achten Sie darauf, dass wir (auch in der Klausur) immer mit „RAD“ rechnen, nie mit „DEG“. Stellen Sie den Taschenrechner bitte entsprechend um.
Das Argument des Sinus (also der Term, der in seinen Klammern steht) ist immer ein Winkelmaß. Es hat keine Einheit. Deshalb können wir nicht einfach eine Zeitverschiebung Δt in das Argument des Sinus schreiben. Wir müssen diese in eine Phasenverschiebung umrechnen. Es gilt:
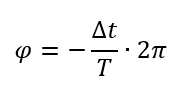
Der Anteil der Verschiebezeit an der Periodendauer Δt/T wird mit einer vollständigen Kreisumdrehung um 2π multipliziert. Damit erhalten wir die Phasenverschiebung zu einer Zeitverschiebung. Achten Sie bitte auf das Minus-Zeichen in der Formel.
In der Anwendung sind noch zwei Zusammenhänge zwischen Sinus und Cosinus wichtig:
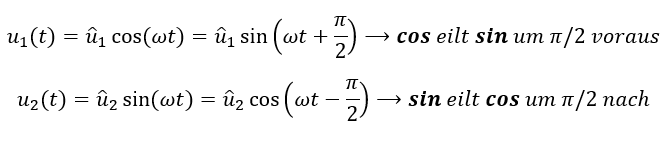
Wir berechnen in diesem Tutorial nur Verläufe sinusförmiger Spannungen und Ströme. Andere Kurvenformen werden nicht betrachtet.
So lange wir nur eine sinusförmige Größe betrachten, ist die Angabe eines Phasenwinkels φ nicht hilfreich. Wir legen dann den Bezugspunkt immer intuitiv so, dass φ = 0 gilt. Das ist möglich, weil die Spannung an der Steckdose keinen zeitlichen Anfang hat, sie ist immer da und sie war auch schon da bevor wir alle geboren wurden. Wenn wir sie messen oder grafisch darstellen, dann legen wir für diesen Vorgang einen Nullpunkt der Zeit fest.
Wenn wir mehr als eine sinusförmige Größe betrachten und diese zeitlich zueinander verschoben sind, dann brauchen wir eine Phase φ, um die Verschiebung auszudrücken.
Bestimmung der Phase
Es gibt ein Verfahren zur Bestimmung der Phasenverschiebung bezogen auf einen Nullpunkt der Zeit. Bei diesem Verfahren bestimmen Sie zunächst die Periodendauer T eines Signals. Das ist die Zeit, zu der sich das Signal wiederholt. Dann zeichnen Sie eine zweite Winkelachse unter die Zeitachse. Der Winkelbereich [0 … 2π] wird so gelegt, dass er dem Zeitbereich [0 .. T] entspricht.
Dann bestimmen Sie den positiven Nulldurchgang des Sinus. Der Sinus hat zwei Nulldurchgänge. Einmal passiert er die 0 von positiven zu negativen Werten hin. Das ist der falsch – der negative Nulldurchgang. Sie suchen den Nulldurchgang, bei dem das Vorzeichen der Werte von negativ zu positiv wechselt.
Anschließend lesen Sie den Winkel ab, bei dem der Sinus seinen positiven Nulldurchgang hat. Dieser Winkel mit negativem Vorzeichen entspricht der Phasenverschiebung der Funktion. Sie müssen ein negatives Vorzeichen nutzen, weil Sie die Verschiebung nach rechts ermittelt haben.
Folgendes Beispiel veranschaulicht das Vorgehen:
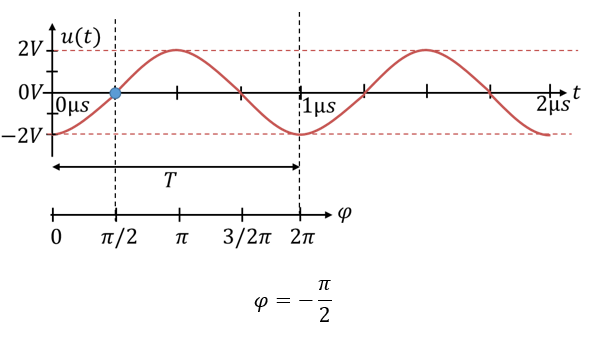
Der Winkel ist immer 2π-periodisch. Ein Winkel von π/2 entspricht auch dem Winkel -3π/2. Sie können den Kreis gegen den Uhrzeigersinn um π/2 entlanglaufen oder im Uhrzeigersinn um 3π/2 entlanglaufen. Sie kommen am gleichen Punkt raus. Deshalb können Sie zur Phasenverschiebung immer 2π addieren oder 2π davon subtrahieren. Es ändert die Information nicht, die in der Phasenverschiebung steckt.
Weitere Wechselgrößen
Nicht nur die Spannung kann eine Wechselgröße sein. Strom und Leistung können ebenfalls Wechselgrößen sein. Zur mathematischen Beschreibung verwenden wir dann andere Vorfaktoren. Beispiele für sinusförmigen Wechselstrom und Wechselleistung sind:
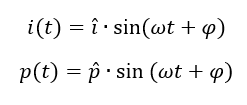
Wir rechnen mit diesen Größen genauso wie mit Wechselspannungen. Sie werden auch genauso gezeichnet.
Beispiel
Ein sinusförmiger Spannungsverlauf wird folgendermaßen als Formel angegeben und über der Zeit dargestellt:
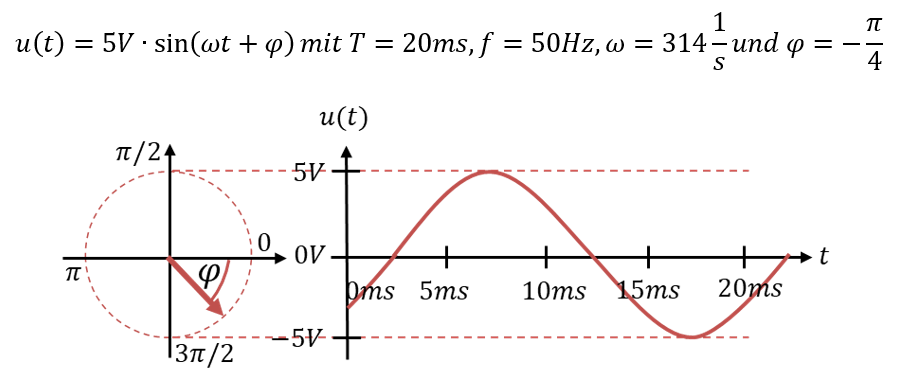
Der Zeiger im linken Teil des Bilds am Kreis startet an der eingezeichneten Position. Der Startwinkel gibt die Zeitverzögerung des Signals an. Der Zeiger wird den Nullpunkt seiner Drehung erst nach 2,5ms erreichen. Der Spitzenwert der Spannung entspricht dem Kreisumfang. Die Amplitude zu einem Zeitpunkt t wird durch die Projektion des Pfeils auf die y-Achse ermittelt. Der Zeiger wandert mit der Zeit t gegen den Uhrzeigersinn den Kreis entlang. Je größer die Kreisfrequenz ω ist, desto schneller dreht sich der Zeiger.
Zusammenfassung
Wir haben folgende Parameter zur Beschreibung der Wechselspannung genutzt:
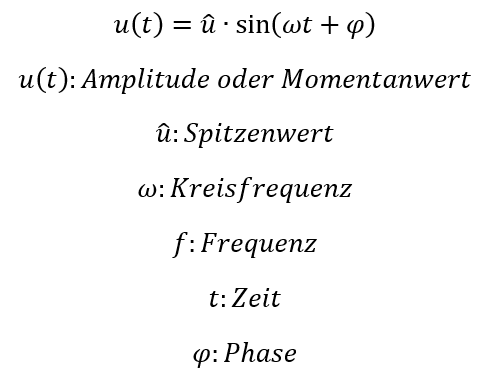
Übungsaufgaben
Als Beispiele gebe ich drei weitere Spannungsverläufe vor. Bitte versuchen Sie, die Formeln zur Beschreibung selbst herauszufinden. Weiter unten finden Sie die Lösungen dazu. Es ist jeweils nur eine Periodendauer als Ausschnitt gezeigt, die Verläufe laufen nach links und rechts genauso weiter wie gezeichnet.
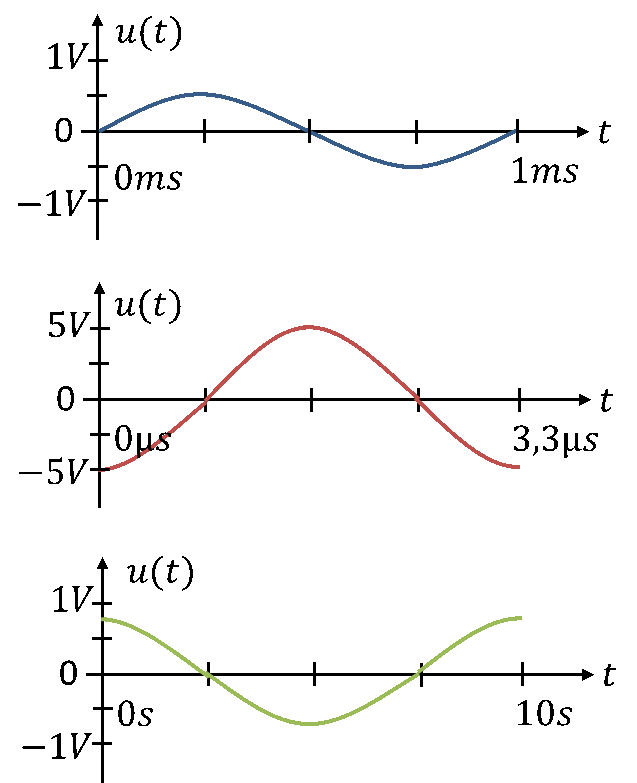
Lösung: