Übertragen wir diese Erkenntnisse auf eine Spule in der Elektrotechnik. Die Spule entspricht dem Wasserrad. Die Trägheit entspricht der Induktivität der Spule. Die Fließgeschwindigkeit des Wassers entspricht dem Strom. Die Steigung des Wassers entspricht der Spannung. Der Strom in der Spule steigt an, wenn eine positive Spannung angelegt wird. Er steigt umso schneller an, je größer die Spannung ist. Der Strom sinkt, wenn die Spannung an der Spule negativ ist.
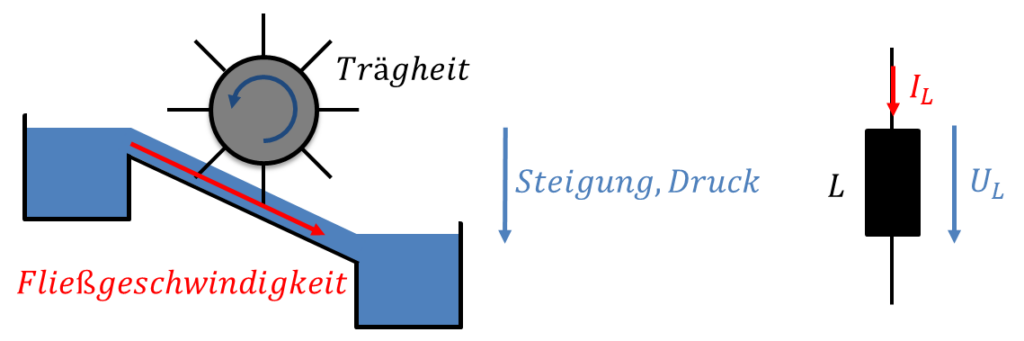
Der Strom durch eine Spule kann nicht einfach angehalten oder abgeschaltet werden, denn die Spule weist eine Trägheit oder einen Schwung auf, der den Strom weitertreibt. Der Strom in einer Spule ändert sich immer nur stetig, er kann nicht springen. Stellen Sie sich bei einer Spule in einer Schaltung vor, dass Ladung von einem trägen Schaufelrad bewegt wird. Das Rad wird durch Spannung in Richtung des Stromflusses schneller und durch Spannung entgegen dem Stromfluss langsamer.
An einer Spule gelten folgende Formeln:
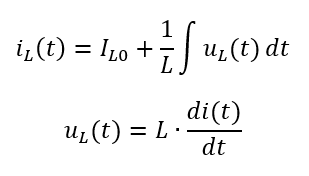
Der Term IL0 bezeichnet den Strom, der bereits in der Spule geflossen ist, bevor Spannung angelegt worden ist. Er steht für die Trägheit bzw. den Schwung, den das Schwungrad bereits hat. Der zweite Integral-Term der Stromgleichung steht für die Änderung des Stroms durch eine Spannung, die über eine Zeit t an der Spule angelegt wird. Das entspricht der Änderung des Schwungs durch Wasserdruck am Schwungrad, das von der Steigung des Wassers am Rad hervorgerufen wird.
Wenn wir an die Spule eine Spannung anlegen, dann ändert sich der Strom, der bereits in der Spule vorhanden war. Wenn wir eine über der Zeit konstante Spannung anlegen, können wir das Integral folgendermaßen vereinfachen:
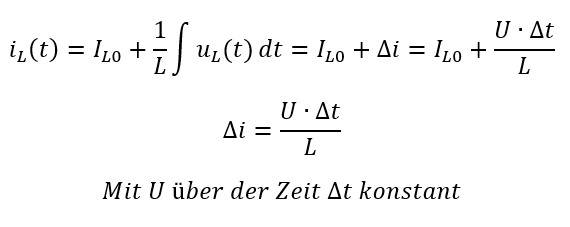
Je länger (t) eine Spannung anliegt und je größer die Spannung (U) ist, desto größer ist der Stromanstieg Δi. Je größer die Induktivität L der Spule ist, desto geringer ist der Stromanstieg.
Legen wir ein paar Beispielspannungen an eine Spule an und analysieren den Stromverlauf. Dafür verwenden wir Spannungsverläufe, die in der Leistungselektronik typisch sind: Getaktete Spannungen.
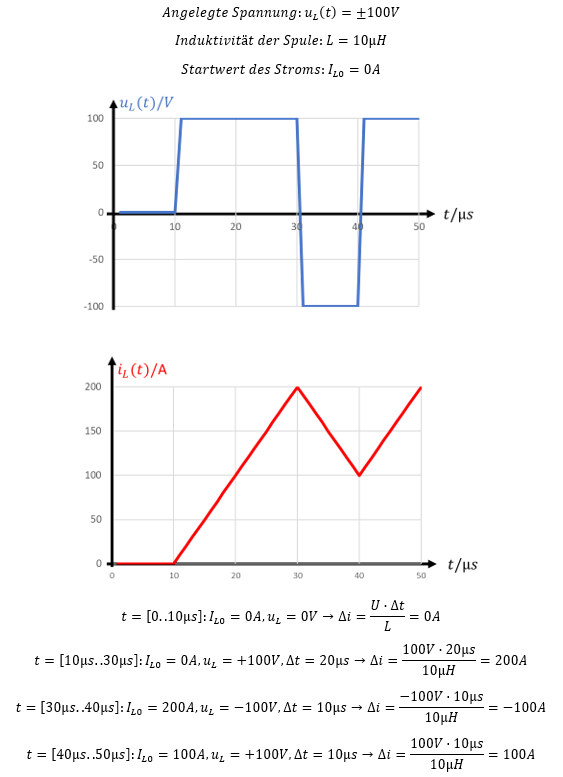
Zu Beginn fließt kein Strom in der Spule. Es liegt auch keine Spannung an der Spule an, die daran etwas ändert. Ab t = 10µs liegen 100V an der Spule an. Der Strom steigt linear an, so lange diese Spannung anliegt. Ist die Spulenspannung negativ, sinkt der Strom. Das ist zwischen 30µs und 40µs der Fall.
Wir berechnen den Stromverlauf abschnittsweise. Ein Abschnitt dauert so lange, wie die Spannung an der Spule einen konstanten Wert aufweist. In jedem Zeitbereich entspricht IL0 dem Stromwert, der am Ende des vorherigen Abschnitts in der Spule fließt. Zu Beginn des zweiten Abschnitts zwischen 10µs und 20µs fließt kein Strom in der Spule, also ist IL0 = 0A.
Am Ende des zweiten Abschnitts hat sich der Strom um Δi = 200A erhöht. Damit weist der Startstrom des dritten Abschnitts zum Zeitpunkt t = 30µs den Wert IL0 = 200A auf. Der Strom ändert sich im dritten Abschnitt um Δi = -100A. Also liegt zu Beginn des vierten Abschnitts bei t = 40µs der Stromstartwert IL0 = 100A vor.
Warum ist der Stromverlauf dreiecksförmig? Das können wir mathematisch über die Stammfunktion zeigen. Man kann es auch nachrechnen. Wir verifizieren dafür als Beispiel den Stromwert zum Zeitpunkt t = 20µs, der mitten im zweiten Abschnitt liegt. Dort gilt:
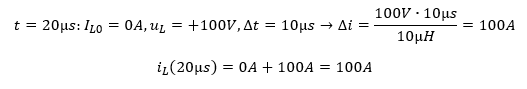
Wir berechnen den Stromwert i(20µs) = 100A mitten im zweiten Abschnitt. Dieser Wert entspricht dem Wert aus dem linearen Stromanstieg, der in rot im unteren Teil der vorherigen Abbildung zu sehen ist. Der Nachweis über die Stammfunktion geht so:

Der Strom verhält sich linear, denn sein Verlauf entspricht mathematisch einer Geradengleichung.
Wenn wir den Strom in einer Spule einstellen wollen, müssen wir folgendes beachten: Wenn der Strom in einer Spule konstant bleiben soll, muss die Spannung 0V betragen. Wenn das nicht möglich ist, sollte die Spannung im Wechsel positiv und negativ sein. Dann schwankt der Strom um einen mittleren Wert herum. Das ist im Zeitbereich zwischen 30µs und 50µs angedeutet.
Die Steigung des Stroms ist größer, wenn die Spannung größer und die Induktivität kleiner ist. Bei einer großen Induktivität brauchen wir also mehr Spannung für eine Stromänderung als bei einer kleinen Induktivität.
Wenn die Beträge der positiven und negativen Spannungen nicht gleich hoch sind, müssen wir die Zeiten anpassen, die die Spannungen jeweils an der Spule anliegen. Gehen wir im nächsten Beispiel davon aus, dass als Spannungen +100V und -40V bereitstehen. In der Spule fließt bereits ein Strom von 100A.
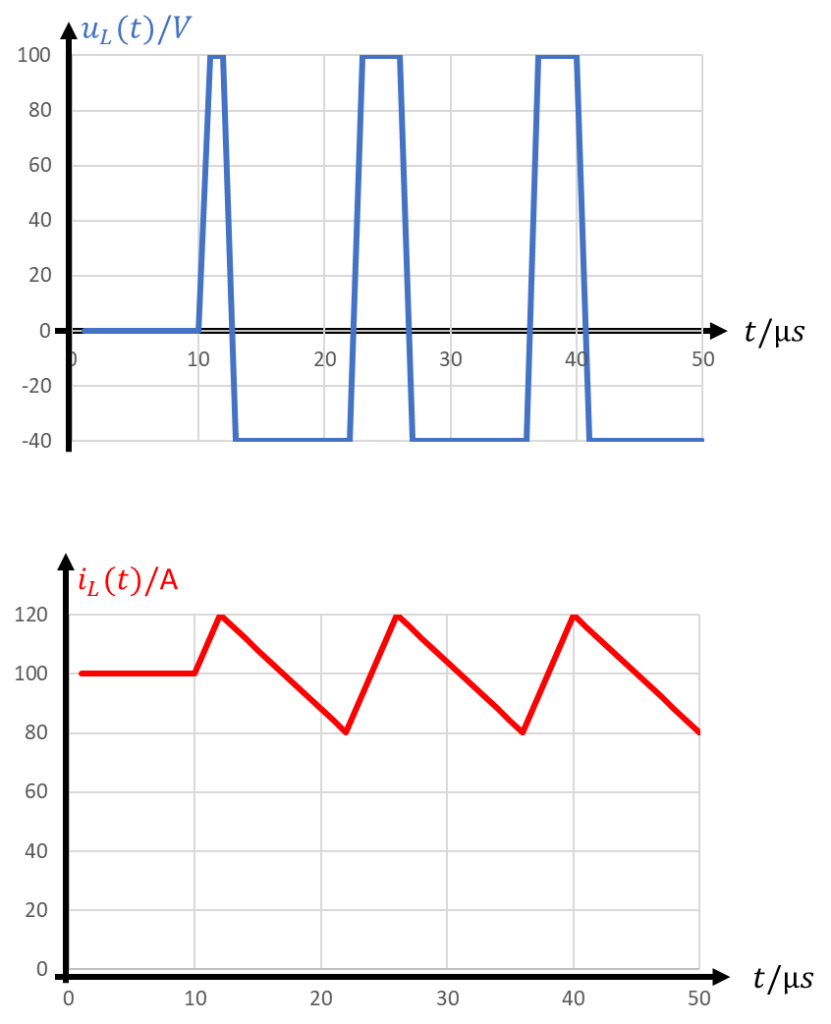
Während der ersten 10 Mikrosekunden ändert sich der Strom nicht, weil keine Spannung an der Spule anliegt. Anschließend liegen entweder +100A oder -40V im Wechsel an der Spule an. Der Stromanstieg (Steigung) bei +100V ist höher als der Abfall des Stroms bei -40V. Deshalb muss für einen konstanten Strom die positive Spannung weniger lange anliegen also die negative Spannung. Es gilt:
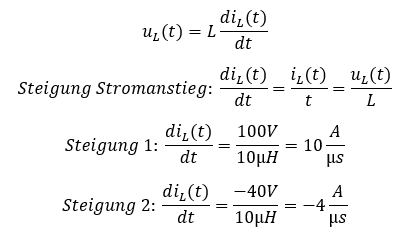
Wenn die +100V also 4µs lang anliegen, beträgt die Stromänderung Δi = 40A. Wenn die -40V für 10µs anliegen, beträgt die Stromänderung Δi = -40A. Damit stellt sich ein dreiecksförmiger Strom ein, der um einen Mittelwert herum schwankt.
Weiter