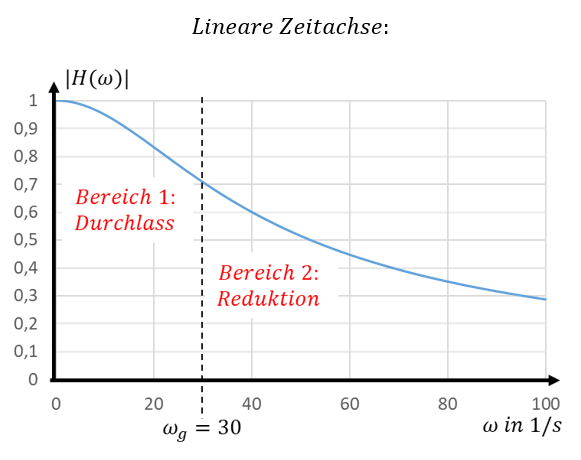
Störfrequenzen und Nutzfrequenzen können sehr kleine oder sehr große Werte annehmen. Wir betrachten Frequenzen mit wenigen Herz (Hz) und solche mit vielen Megaherz (MHz). Wir betrachten also auch Kreisfrequenzen ω = 2πf im Bereich ω = 1/s bis zu ω = M 1/s. Um diese gleichzeitig in einem Diagramm abbilden zu können, nutzen wir eine logarithmische Frequenzachse. Die Frequenz nimmt auf dieser Achse von einem vertikalen Strich zum nächsten um Faktor 10 zu. Bei linearen Achsen wird im Beispiel von einem Strich zum nächsten +10 gerechnet. Mit der logarithmischen Frequenzachse können wir größere Frequenzbereiche in einem Diagramm darstellen.
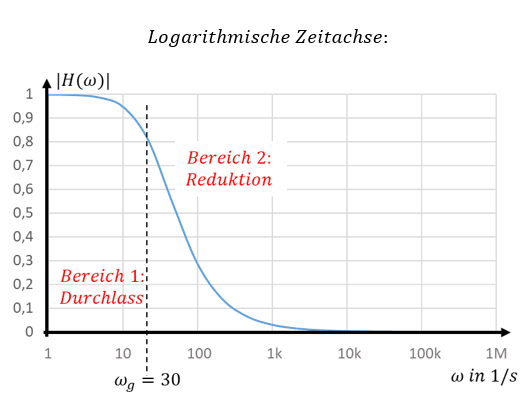
Der Betrag der Übertragungsfunktion ist jetzt für einen viel weiteren Frequenzbereich von ω = 1 1/s bis ω = 1M 1/s dargestellt. Die Übertragungsfunktion des Filters kann bei sehr großen Frequenzen ω > 10000 allerdings nicht mehr abgelesen werden. Die y-Werte sind zu klein. In der Darstellung der Frequenzen im Bereich ω = [0 … 100 1/s] ist das nicht aufgefallen, hier waren die y-Werte einfach nicht so klein.
Um winzige Zahlenwerte noch von 0 unterscheiden zu können, ändern wir die y-Achse ebenfalls hin zu einer logarithmischen Skala. Hier wird der Achsenwert zwischen zwei horizontalen Strichen um Faktor 10 erhöht statt bisher um +0,1. Die gleiche Übertragungsfunktion sieht dann folgendermaßen aus:
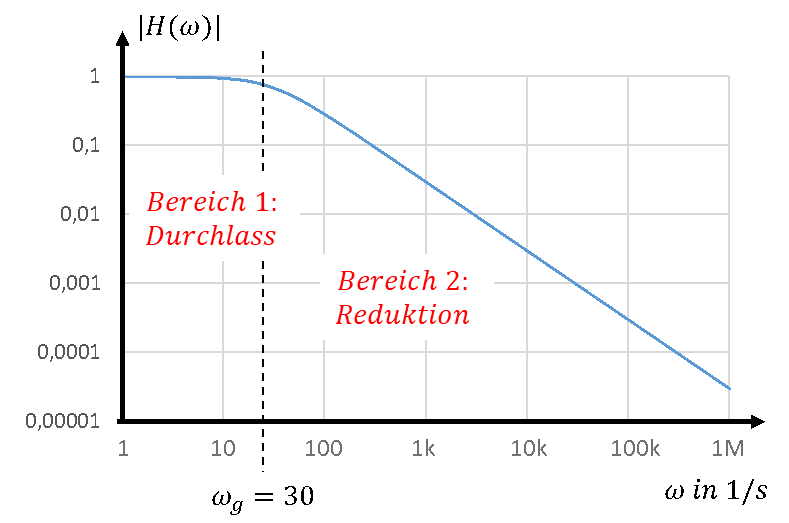
In dieser Darstellungsform können wir über einen sehr weiten Frequenzbereich auch sehr kleine Übertragungsfunktionswerte visualisieren. In dieser doppelt-logarithmischen Darstellung werden Übertragungsfunktionen von Filtern üblicherweise dargestellt. In dieser Darstellung erkennen Sie auch besser, warum die Grenzfrequenz die Übertragungsfunktion in zwei Bereiche unterteilt. Links von der Grenzfrequenz ist der Betrag der Übertragungsfunktion etwa gleich 1. Rechts von der Grenzfrequenz fällt der Betrag der Übertragungsfunktion linear ab.
Eigentlich sinkt die Übertragungsfunktion mit über der Frequenz mit dem Verhalten H~1/f. In der doppelt-logarithmischen Darstellung sieht dieses Verhalten aus wie eine Gerade. Das ist für unser Gehirn einfacher zu verarbeiten. Darin können wir leichter Werte ablesen und das können wir leichter zeichnen. Behalten Sie im Hinterkopf, dass es sich nur um einen grafischen Trick handelt, der nur in der doppelt-logarithmischen Darstellung funktioniert. Das Verhalten ist nicht linear, es sieht nur so aus.
Dieses doppelt-logarithmische Diagramm aus Übertragungsfunktion und Kreisfrequenz wird als „Bode-Diagramm“ bezeichnet.
Betrachtung des Phasenwinkels
Dieser Unterpunkt zur Phase ist nicht klausurrelevant.
Die Übertragungsfunktion H(ω) ist eine komplexe Größe. Komplexe Größen bestehen aus Betrag und Phase. Da die Übertragungsfunktion des Filters den Drehoperator j enthält, dreht ein Filter offenbar auch die Phase eines Eingangssignals. Die folgende Abbildung zeigt die Phase der Übertragungsfunktion über der Kreisfrequenz. Die Phase ändert sich mit steigendem ω von 0° auf -90°.
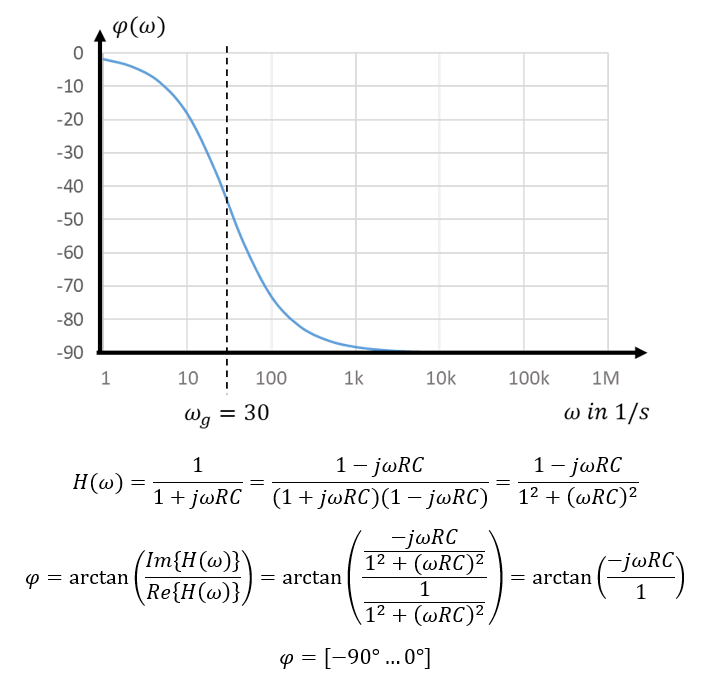
Bode-Näherung
Das Filter dämpft ein Signal mit der Grenzfrequenz bereits um den Faktor 0,7. Die Dämpfung bei Frequenzen in der Nähe der Eckfrequenz ist schwierig zu berechnen. Weit links davon beträgt die Übertragungsfunktion konstant 1, weit rechts davon fällt sie mit konstanter Steigung ab. Das ist beides mathematisch beherrschbar.
Wir nutzen an der Grenzfrequenz die Bode-Näherung als Vereinfachung. Wir tun so, als ob die Übertragungsfunktion bei Frequenzen kleiner oder gleich der Grenzfrequenz immer 1 betragen würde. Bei Frequenzen größer als der Grenzfrequenz würde sie direkt mit konstanter Steigung sinken. Das sähe etwa so aus:
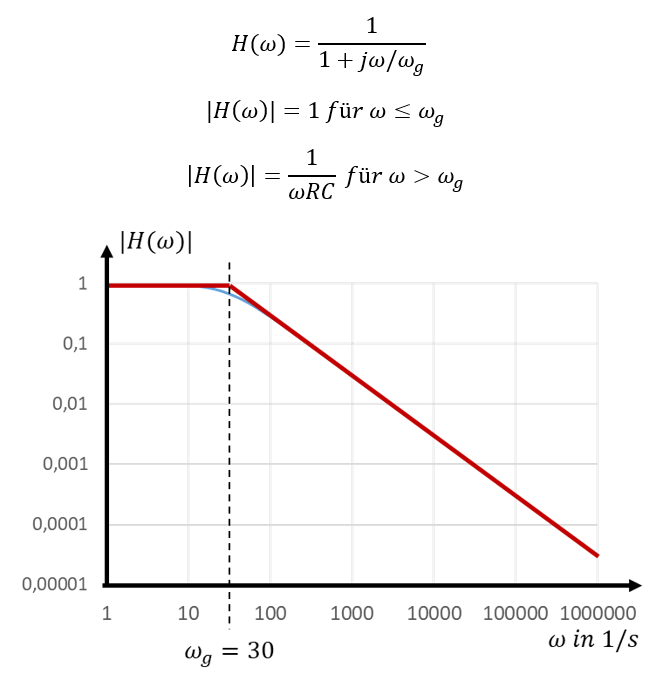
In rot sehen Sie den Verlauf der Übertragungsfunktion nach Bode-Näherung. In blau darunter den realen Verlauf. Mit der Bode-Näherung machen wir nur rund um die Grenzfrequenz einen Fehler. Sonst sind beide Kurven nahezu deckungsgleich. Da wir später den Bereich rund um die Grenzfrequenz sowieso meiden werden, werden wir diese Näherung ab jetzt zur mathematischen Vereinfachung nutzen.
Rechts von der Grenzfrequenz gilt:
Das Bode-Diagramm der Übertragungsfunktion besteht ab jetzt nur noch aus 2 Geraden. Vergleichen Sie es mal mit der ersten Version mit den linearen Achsen. So fällt das Arbeiten damit deutlich leichter. Wir können direkt ablesen, wie das Filter die Eingangssignale verändert. Wählen Sie die Kreisfrequenz des Eingangssignals auf der x-Achse. Lesen Sie den zugehörigen Betrag der Übertragungsfunktion auf der y-Achse ab. Mit diesem Faktor wird der Spitzenwert des Signals multipliziert. Das ist viel einfacher, als die Formel der Übertragungsfunktion für das ω des Signals zu berechnen.
Beim Verlauf der Phase der Übertragungsfunktion wird ebenfalls genähert, damit wir auch hier mit Geraden rechnen können. Die Näherung ist so krass, dass wir damit die Phasen wirklich nur abschätzen können. Das genügt in der Praxis meistens. Die Phase wird in der Prüfung nicht betrachtet.
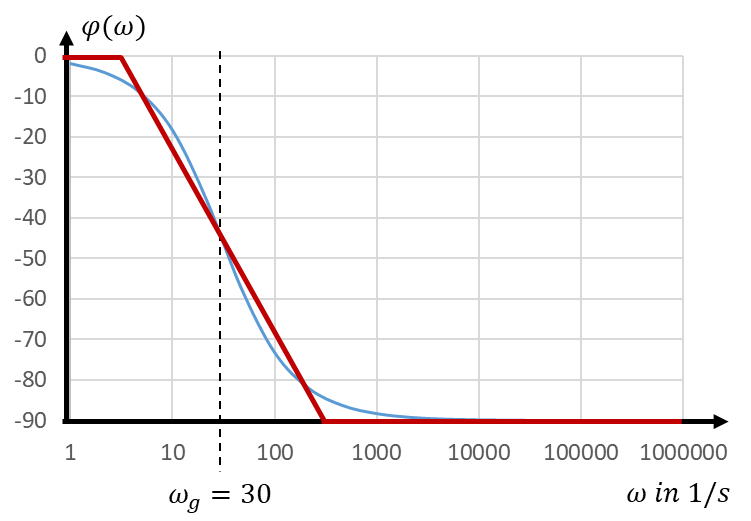
Die Phase ist zunächst konstant bei 0. Sie beginnt nach der Bode-Näherung bei der Frequenz ω = 0,1 ∙ ωg linear zu fallen. Sie wird bei der Frequenz ω = 10 ∙ ωg wieder waagerecht. In diesem Fall sinkt die Phase zwischen ω = 3 1/s und ω = 300 1/s. An der Grenzfrequenz beträgt die Phase -45°. Den realen Verlauf sehen Sie in blau unter der roten Kurve. Die Phase wird linear dargestellt. Sie ändert sich nicht so stark, dass eine logarithmische Achse sich lohnt.
Weiter