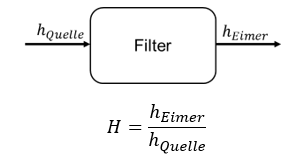
Filterwirkung einer Heizung
Es gibt ein gutes Beispiel aus dem Alltag, an dem man die Wirkung eines Filters anschaulich erkennt. Wir betrachten dafür einen normalen Heizkörper mit einem Dreh-Ventil, das Sie von Hand auf- und zudrehen können. Wenn Sie aufdrehen, wird der Heizkörper warm. Der Eingang des Systems ist das Ventil. Der Ausgang ist die Temperatur des Heizkörpers.
Wenn Sie den Heizkörper jede Sekunde einmal vollständig aufdrehen und ihn dann wieder vollständig schließen, wie ändert sich dann seine Temperatur? Gar nicht. So schnelle Änderungen mit 1Hz am Ventil führen nicht dazu, dass der Heizkörper genauso schnell seine Temperatur ändert. Wenn Sie das gleiche Ventil am Heizkörper alle halbe Stunde voll aufdrehen und dann wieder nach einer halben Stunde schließen, dann ändert sich die Temperatur des Heizkörpers. Er wird abwechselnd warm und kalt.
Eine schnelle Änderung der Eingangsgröße (Ventilstellung) führt nicht zu einer Änderung der Ausgangsgröße (Temperatur). Schnelle oder hochfrequente Signale am Eingang sind am Ausgang nicht sichtbar. Eine langsame oder niederfrequente Änderung am Eingang alle halbe Stunde ist am Ausgang sichtbar. Damit bildet eine Heizung ein Filter, denn die Ausgangsgröße verändert die Eingangsgröße abhängig von der Signalfrequenz.
Der Rest dieses Kapitels ist für die Prüfung nicht relevant. Hier wird versucht, die Wirkung von Filtern am Wassermodell anschaulich zu erklären. Wenn Sie sich mit wenig Aufwand nur auf die Vorlesung vorbereiten wollen, dann lassen Sie den kompletten Rest von „Filter verstehen“ einfach weg.
Wassermodell des Filters
Viele elektrotechnische Zusammenhänge von Spannung und Strom können am Wassermodell visualisiert werden. Einige Studierende empfinden allerdings die Erklärung von Filtern am Wassermodell als wenig hilfreich. Wenn Sie merken, dass das Wassermodell Ihnen nicht beim Verständnis hilft, dann überspringen Sie dieses Kapitel einfach.
Wir betrachten für die anschauliche Erklärung der Funktionsweise von Filtern das Wassermodell aus Grundlagen der Elektrotechnik. Wenn dieser Kurs bei Ihnen lange her ist, nehmen Sie sich die Zeit, das Kapitel nochmal zu lesen. Wir zeigen am Wassermodell die Wirkung von Filtern. Danach verstehen Sie diese auch bei elektrischen Filtern.
Betrachten wir Wechselsignale im Wassermodell. Um Sensoren nachbilden zu können, brauchen wir Wechselspannungsquellen. Wir brauchen eine Wasserquelle, deren Ausgangswert sich sinusförmig ändert. Im Wassermodell ist das ein riesiger See, deren Höhe sich sinusförmig ändert. Wir betrachten keine negativen Spannungen, also keine negativen Höhen im Wassermodell. Das wäre zu kompliziert. Eine Quelle, deren Höhe sich zeitlich verändert, kann folgendermaßen visualisiert werden:
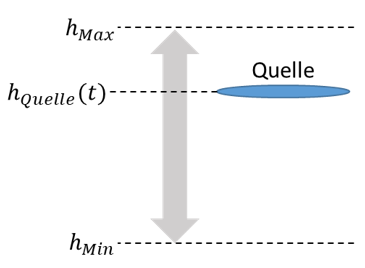
Um negative Höhen zu vermeiden, setzen wir hMin = 0m. Die Höhe von Wasser ist analog zur Spannung in der Elektrotechnik. Je höher der See gezeichnet ist, desto höher ist die Spannung der elektrischen Spannungsquelle, die der See veranschaulicht. An einem elektrischen Filter liegen auch negative Spannungen an.
Filter bestehen immer aus der Kombination aus begrenzenden Elementen wie z. B. Widerständen und Speichern in einem Schaltungsteil. Beim Wassermodell steht ein Rohr für einen Ohm`schen Widerstand. Der Widerstandswert steigt mit kleinerem Durchmesser des Rohrs an. Die Steigung des Rohrs steht für die Spannung am Widerstand. Der Wasserfluss (Stromfluss) durch das Rohr wird durch seine Steigung und seinen Durchmesser bestimmt.
Der Eimer ist der Speicher im Wassermodell. An einem Eimer ist der Füllstand die Spannung und der Zu-/Ablauf der Strom.
Modellierung eines Filters
Es wird ein Rohr zwischen einer Quelle und einem Eimer verbaut. Die Höhe der Quelle ist veränderlich. Die Höhe des Eimers nicht, aber der Füllstand des Eimers kann seine Höhe ändern. Das Rohr ist an der einen Seite an der Quelle befestigt. Ändert die Quelle ihre Höhe, bewegt sich dieses Ende des Rohrs mit auf und ab. Die andere Seite des Rohrs ist am Eimer befestigt. Es schwimmt auf dem Wasser. Es ändert seine Höhe immer mit dem Füllstand des Eimers. Beide Seiten des Rohres können also ihre Höhe ändern.
In den folgenden Abbildungen sind mehrere Paarungen von Eimerfüllstand und Quellenhöhe dargestellt. Wichtig ist jeweils, in welche Richtung das Wasser fließt und wie hoch die Höhendifferenz am Rohr ist. Daraus ermitteln wir die Zulauf- und Ablaufgeschwindigkeit des Eimers.
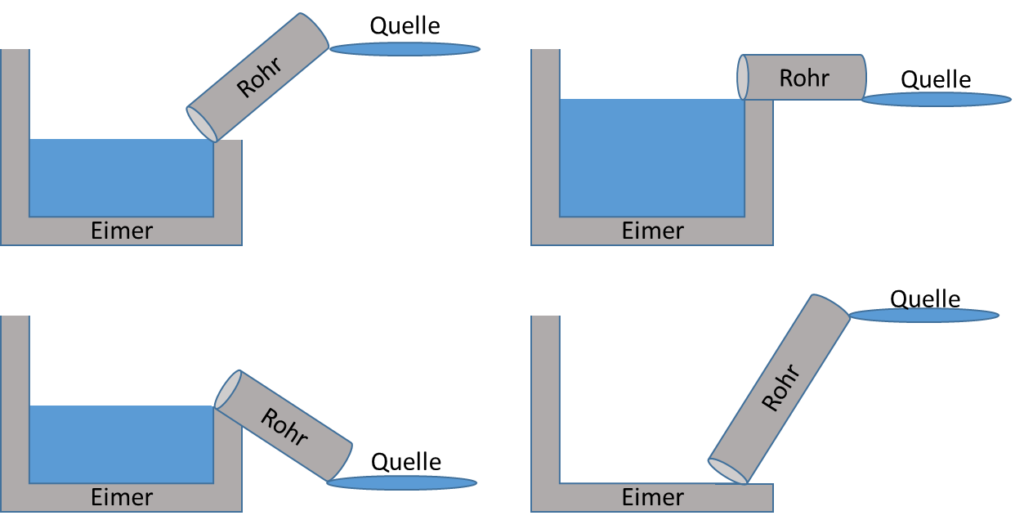
In der Abbildung oben links wird der halb gefüllte Eimer aus einer Quelle gefüllt, deren Höhe oberhalb des Eimerfüllstands liegt. Es fließt weiteres Wasser aus der Quelle in den Eimer. In der Abbildung unten links ist der Eimer ebenfalls halb gefüllt. Die Höhe der Quelle ist unterhalb der Höhe des Eimerfüllstands. Es fließt Wasser aus dem Eimer in die Quelle. Die Abbildung oben rechts zeigt einen Fall gleicher Höhe von Eimerfüllstand und Quelle. Es fließt kein Wasser. Dieser Zustand kann auf jeder Höhe erreicht werden.
Der Zulauf von Wasser von der Quelle in den Eimer (oder umgekehrt) ist in diesem System begrenzt. Er ist in der Abbildung unten rechts maximal groß und in Richtung Eimer orientiert. Dafür muss die Quelle auf maximaler Höhe sein und der Eimer muss vollständig leer sein. Mehr Wasser kann nicht durch das Rohr fließen als in diesem Fall. Die Geschwindigkeit von Zufluss und Abfluss bestimmen, wie schnell sich der Füllstand des Eimers ändert. Sie wird von der Steigung des Rohrs vorgegeben.
Die rechte Wand des Eimers ist in den Darstellungen im Weg. Sie bewegt sich einfach immer so, dass Wasser fließen kann. Wenn der Füllstand des Eimers sinkt, geht die Wand ein Stück weiter runter, so dass er weiter sinken kann. Diese Wand ist also nie im Weg. Die Analogie mit dem Wasser ist für Filter nicht perfekt, sie benötigt leider diese unschöne Lösung.
Um ein Wechselsignal zu erzeugen, wird die Quelle jetzt sinusförmig hoch- und runterbewegt. Dadurch ändern sich ständig Intensität und Richtung des Wasserflusses in den Eimer. Dies ändert ständig den Füllstand des Eimers.
Der Füllstand des Eimers folgt der Höhe der Quelle. Über das Rohr sind beide miteinander verkoppelt. Quelle, Rohr und Eimer bilden eine Reihenschaltung.
Beeinflussung des Filters
Den Spitzenwert des Füllstandes des Eimers können wir über drei Parameter beeinflussen. Wir ändern in Gedanken immer einen der Parameter, die anderen beiden halten wir dabei unverändert.
1. Rohrdurchmesser: Wenn wir einen Eimer durch einen Strohhalm mit sehr kleinem Durchmesser befüllen, dann dauert dies lange. Der Füllstand des Eimers ändert sich langsamer als bei einem Rohr mit großem Durchmesser.
2. Grundfläche des Eimers: Wenn wir statt dem Eimer ein Schwimmbecken füllen, dann ändert sich der Füllstand weniger stark. Der Füllstand ändert sich erneut langsamer bei einem Eimer mit größerer Grundfläche.
3. Frequenz: Wenn wir die Höhe der Quelle schneller verändern, dann erhöhen wir die Frequenz des Signals an der Quelle. Es ist dann weniger Zeit verfügbar, um den Eimer zu füllen und zu leeren. Es wird pro Sinus-Halbwelle weniger Wasser durch das Rohr bewegt als bei einer langsamen Bewegung. Das liegt an der Begrenzung des maximalen Wasserflusses durch den Rohrdurchmesser.
Wenn das Rohr dünn ist und die Grundfläche des Eimers groß ist, dann kommt der Füllstand des Eimers bei hoher Sinus-Frequenz nicht mehr mit. Der Eimer wird nicht mehr vollständig geleert und gefüllt. Der Füllstand des Eimers hinkt der Höhe der Quelle zeitlich hinterher. Dieser Effekt wird beim Filtern ausgenutzt. Um ihn geht es in diesem Kapitel.
Wir beginnen die Betrachtung mit geringer Frequenz, großem Rohrdurchmesser und kleiner Eimerfläche. Wir befüllen also einen winzigen Fingerhut sehr langsam durch ein richtig großes Abwasserrohr. Die Begrenzung des Wasserflusses ist viel kleiner als der notwendige Wasserfluss, mit dem der Füllstand des Eimers stets auf Quellenhöhe gehalten wird. Der Füllstand des Eimers ändert sich deshalb nahezu ohne zeitliche Verzögerung, sobald sich die Höhe der Quelle ändert.
Der Spitzenwert der Quellenbewegung ist so gewählt, dass der Eimer immer vollständig gefüllt und vollständig geleert wird. Die Quellenhöhe „Max“ ist also so hoch, dass der Eimer vollständig gefüllt wird. Die Quellenhöhe „Min“ entspricht der Höhe des Bodens des Eimers. Ein Zeitverlauf des Befüllens und Leerens sieht folgendermaßen aus:
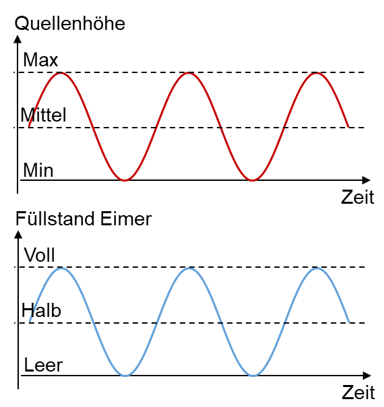
Wir nehmen jetzt einen dünneren Strohhalm als Rohr, einen viel größeren Eimer und wir bewegen die Quelle schneller hoch und runter. Die Begrenzung des Wasserflusses ist jetzt größer als der notwendige Wasserfluss, mit dem der Füllstand des Eimers stets auf Quellenhöhe gehalten wird. Der Füllstand des Eimers erreicht deshalb nicht mehr die Spitzenwerte voll und leer. Er folgt der Höhe der Quelle zeitversetzt. Dann sieht ein Zeitverlauf etwa folgendermaßen aus:
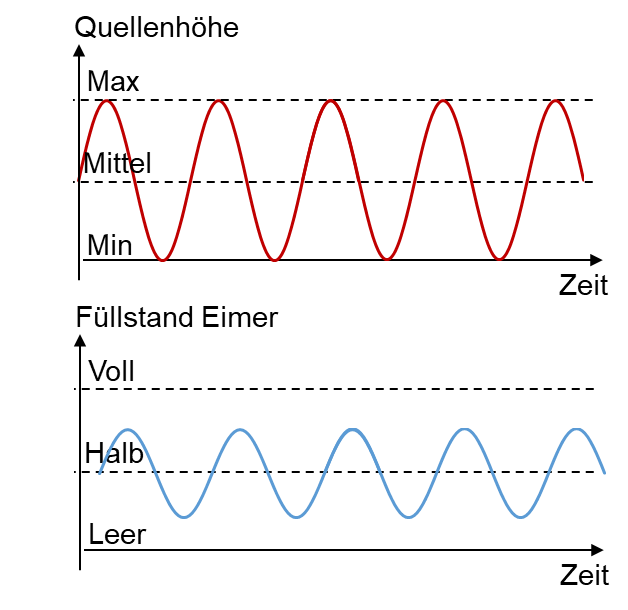
Wir erhalten eine Phasenverschiebung zwischen Quellenhöhe und Eimerfüllstand. Der Spitzenwert des Eimerfüllstands ist geringer als der der Quellenhöhe. Um diesen Effekt weiter zu intensivieren, reduzieren wir die Querschnittsfläche des Rohrs, wir erhöhen die Fläche des Eimers oder wir erhöhen die Frequenz des Sinus der Quelle.
Je schneller sich die Höhe der Quelle ändert, desto weniger stark ändert sich der Füllstand des Eimers. Damit haben wir bereits ein Filter gebaut. Die Eingangsgröße des Filters ist die Quellenhöhe. Die Ausgangsgröße ist der Füllstand des Eimers. Das Filter wirkt unterschiedlich auf Signale abhängig von ihrer Frequenz. Je höher die Frequenz der Signale am Eingang ist, desto geringer ist der Spitzenwert der Signale am Ausgang des Filters.
Nutzsignal und Störsignal
Stellen Sie sich vor, dass die Quelle zwei Signale enthält: Ein niederfrequentes Nutzsignal und ein hochfrequentes Störsignal. Die Quelle bewegt sich langsam mit dem Nutzsignal auf und ab. Es weist die Frequenz fNutz und den Spitzenwert hNutz auf. Diese Bewegung wird von einer schnellen Bewegung mit der Frequenz fStör und dem Spitzenwert hStör des Störsignals überlagert. Die konstante Höhe hMittel brauchen wir in der Formel, damit sich die Höhe als Wechselsignal um die mittlere Höhe herumbewegt.
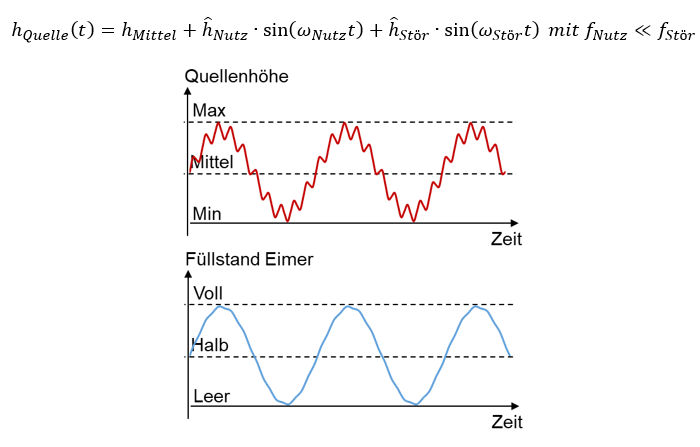
Der Füllstand des Eimers folgt dem langsamen Nutzsignals vollständig. Weil sich die Quellenhöhe langsam ändert, wird viel Wasser bewegt. Das Rohr ist dick genug, um mit diesem Wasser die Füllhöhe des Eimers zu verändern, weil seine Fläche bezogen auf die bewegte Wassermenge klein ist.
Das schnelle Störsignal muss durch das gleiche Rohr hindurch und den gleichen Eimer füllen. Es wird bei der hohen Frequenz aber viel weniger Wasser bewegt. Das Rohr ist zu dünn, um mit der geringen Wassermenge bei der großen Fläche des Eimers dessen Füllstand nennenswert zu ändern. Deshalb ist das Störsignal im Füllstand des Eimers weniger stark zu erkennen als in der Quellenhöhe.
Wir können über Rohrdurchmesser und Eimerfläche beeinflussen, bis zu welcher Frequenz Signale der Quelle noch vollständig im Eimerfüllstand zu sehen sein sollen. Wenn wir also wissen, welche Frequenz Störsignal und Nutzsignal haben, können wir Eimer und Rohr entsprechend anpassen. So baut man Filter. Wenn das Filter einmal aufgebaut ist, dann sind Rohrdurchmesser und Eimerfläche unveränderliche Parameter. Nur die Frequenz, mit der die Quellenhöhe verändert wird, ändert sich dann mit den angelegten Signalen.
Betrachten wir ein Blockschaltbild des Aufbaus. Die Quellenspannung ist die Eingangsgröße. Der Füllstand des Eimers die Ausgangsgröße. Wir definieren für das Filter eine Übertragungsfunktion. In dieser steckt die Mathematik der Filter, die wir als nächstes betrachten werden.