Es gibt viele Faktoren, die auf die Messunsicherheit eines Systems wirken. Hier ein Ausschnitt:
Reproduzierbarkeit
Eine Messung ist gut reproduzierbar, wenn mehrere nacheinander ablaufende Messungen unter gleichen Umständen zueinander nur eine geringe Abweichung aufweisen. Die Ergebnisse mehrerer Messungen sollten idealerweise gleich sein. Das ist in der Praxis aber nie der Fall. Wenn eine Messung schlecht reproduzierbar ist, dann können wir ihr nicht trauen. Wenn schon unter unveränderten Randbedingungen die Ergebnisse schwanken, dann schwanken diese wahrscheinlich umso schlimmer, wenn auch noch die Randbedingungen variieren. Die Reproduzierbarkeit ist Teil der Messunsicherheit. Je geringer die Reproduzierbarkeit ist, desto größer ist die Messunsicherheit.
Querabhängigkeit
In der Physik hängen viele Größen miteinander zusammen bzw. voneinander ab. Der Ohm´sche Widerstand eines Drahts hängt z. B. von der Temperatur des Drahts ab. Ein kalter Kupferdraht hat einen kleineren Widerstand als ein warmer Draht. Das hängt vom Material – hier Kupfer – ab. Wenn wir den Widerstandswert messen, müssen wir berücksichtigen, bei welcher Temperatur wir gemessen haben.
Der Draht hat also gar nicht einen festen Widerstandswert, sondern viele unterschiedliche Werte. Wie können wir dann einen Wert als wahr bezeichnen? Am einfachsten lösen wir dieses Problem, indem wir jeden Draht bei einer Referenztemperatur von z. B. 25°C messen. Damit sind unterschiedliche Drähte wieder vergleichbar. Die Herausforderung besteht dann darin, die Temperatur des Drahts ausreichend genau vorzugeben. Dazu können wir ihn z. B. in einen Klimaschrank (eine Art Backofen) legen. Sie sehen schon, der Aufwand ist groß.
Wir können auch die Temperaturabhängigkeit des Drahtmaterials ermitteln. Dann messen wir den Widerstandswert bei irgendeiner Temperatur und korrigieren den gemessenen Wert mit einer Formel für die Temperaturabhängigkeit. Betrachten wir einen Draht, der bei 25°C den Widerstandswert R0=1kΩ aufweist. Welchen Widerstandswert weist der bei T = 100°C auf? Es gelten folgende Formeln für Kupfer:

Der Widerstandswert eines Kupferdrahts ist stark abhängig von der Temperatur. Diesen Effekt bezeichnen wir als Querabhängigkeit.
Das Problem stellt sich normalerweise anders herum. Wir messen einen Widerstand in der Praxis z. B. bei T = 100°C. Wir geben Widerstandswerte aber immer bei der Referenztemperatur von T = 25°C an. Sonst gäbe es ja nicht einen „richtigen“ Wert. Deshalb müssen wir den gemessenen Wert auf die Referenztemperatur umrechnen. Dafür drehen wir die Formel oben um. Wir suchen eigentlich den Wert R0. Das ist der Widerstandswert bei 25°C. Gegeben haben wir den Widerstandswert bei T = 100°C – den haben wir gemessen.
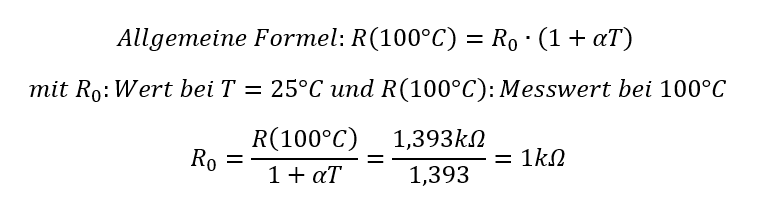
Durch Umstellen der Formel bekommen wir den bei der „falschen“ Temperatur gemessenen Widerstandswert auf den „richtigen“ Wert bei Referenztemperatur umgerechnet. Sie erkennen auch am Zahlenbeispiel, dass wir durch die mathematische Kompensation den Einfluss der Temperatur auf die Messung eliminiert haben. Der Draht hatte ja von vorne herein einen Widerstandswert von 1kΩ. Wir waren nur so blöd, den Wert bei T = 100°C statt bei 25°C zu messen. Wir haben dadurch einen falschen Wert ermittelt.
Als Querabhängigkeit einer Messung bezeichnen wir allgemein den Einfluss anderer physikalischer Größen auf das Messergebnis. Fast alle Messungen sind abhängig von der Temperatur. Einige sind noch abhängig vom Druck. Sie müssen die spezifische Querabhängigkeit jeder Messung und deren Kompensation ermitteln (googlen), bevor Sie eine Messung durchführen.
Querabhängigkeiten erhöhen die Messunsicherheit. Sie werden manchmal separat zur Messunsicherheit aller anderen Einflussgrößen angegeben. Dann gibt es zwei Angaben zur Messunsicherheit. Wenn nur ein einziger Wert für eine Messunsicherheit angegeben ist, dann sind die Querabhängigkeiten da bereits eingerechnet.
Weiter