Ähnlichkeit
Viele reale technische Systeme verhalten sich ähnlich. Wir beschreiben ähnliche Systeme mit der gleichen Formel, in die wir andere Parameter einsetzen. Ein Beispiel ist die Geradengleichung. Mit ihr können Sie sehr unterschiedliche Systeme ausrechnen. Dafür setzen Sie dann jeweils passende Parameter m und b ein. Es gilt allgemein für alle linearen Systeme:

Welche Systeme können mit der Geradengleichung berechnet werden? Naja, alle linearen Systeme, denn die Geradengleichung ist linear. Wir suchen in diesem Kapitel neben Linearität weitere Systemeigenschaften, die deren Verhalten charakterisieren. Dazu gibt es dann immer eine allgemeine Formel, um alle Systeme mit diesem Verhalten zu berechnen. Zu der allgemeinen Formel gibt es charakteristische Parameter, mit denen Sie die allgemeine Formel auf ihr Problem anpassen.
Übertragungsfunktion
Die Übertragungsfunktion gibt an, wie eine Eingangsgröße durch ein System oder einen Funktionsblock verändert wird. Die Ausgangsgröße ist i. A. anders als die Eingangsgröße. Die Übertragungsfunktion H beschreibt die Veränderung der Eingangsgröße mathematisch. An H erkennen wir den Typ der Verhaltensweise des Systems.
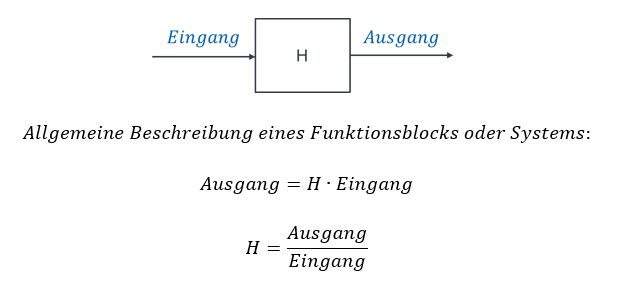
Proportionalität
Wir starten mit dem einfachsten Verhaltenstyp: Dem proportionalen Verhalten. Bei Systemen mit proportionalem Verhalten ist die Ausgangsgröße proportional zur Eingangsgröße. Proportionales Verhalten wird in der Regelungstechnik mit „P-Verhalten“ abgekürzt. Bei proportionalem Verhalten ist die Übertragungsfunktion H eine Konstante:
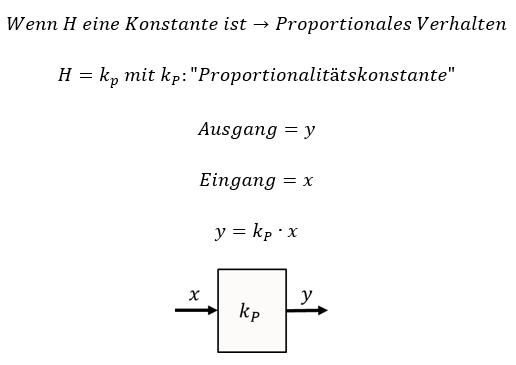
Einen Funktionsblock mit P-Verhalten modellieren wir in einem Regelkreis als Quadrat mit dem Bezeichner kP im Zentrum. Hier kann auch an Stelle des Bezeichners kP direkt der Zahlenwert von kP stehen.
Die Gleichung zwischen Ausgang und Eingang eines Systems mit proportionalem Verhalten ist ein Sonderfall der Geradengleichung.

Die Steigung m entspricht der Proportionalitätskonstanten kP. Ein System, dessen Eingangs- und Ausgangsgröße eine Geradengleichung erfüllen, verhält sich linear. Ein lineares Verhalten mit b = 0 wird als proportionales Verhalten bezeichnet. Werden Eingangs- und Ausgangsgröße gegeneinander aufgetragen, dann ergibt sich für z. B. kP = 3 folgendes Bild:
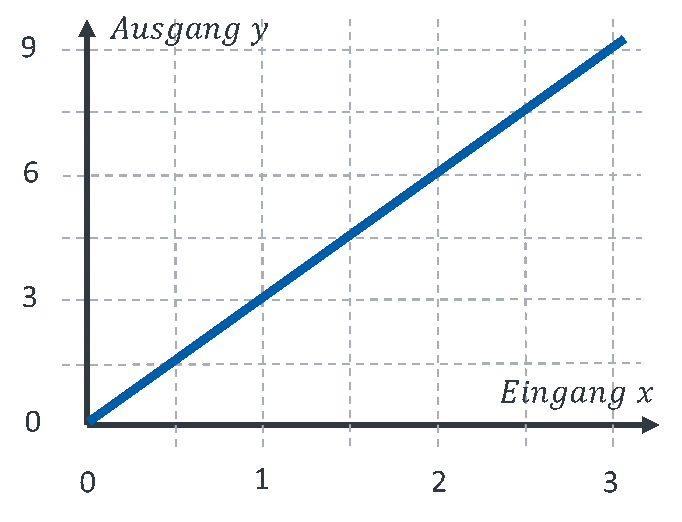
Ist der Eingang gleich 0, ist auch der Ausgang gleich 0. Steigt die Eingangsgröße, dann steigt auch die Ausgangsgröße. Dies ist charakteristisch für proportionales Verhalten. Bei z. B. kP = 3 ist der Ausgangswert drei Mal so hoch wie der Eingangswert.
Mit dem Parameter kp ist ein proportionales System aus Sicht der Regelungstechnik vollständig beschrieben. Wenn Sie ein System mit P-Verhalten modellieren, dann definieren Sie dessen Eingangsgröße x(t) und seine Ausgangsgröße y(t). Der Parameter kp entspricht dem Quotienten aus Ausganggröße y geteilt durch die Eingangsgröße x. kp entspricht also der Übertragungsfunktion H.
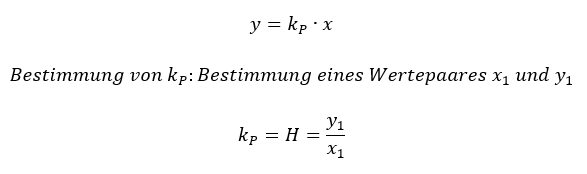
Nach der allgemeinen Definition betrachten wir einige Beispiele.
Beispiel Widerstand
Der Zusammenhang zwischen Spannung und Strom an einem Widerstand in der Elektrotechnik ist proportional. Definieren wir die Spannung als Ausgang und den Strom als Eingang des Funktionsblocks Widerstand, dann bildet der Widerstandswert R die Proportionalitätskonstante.
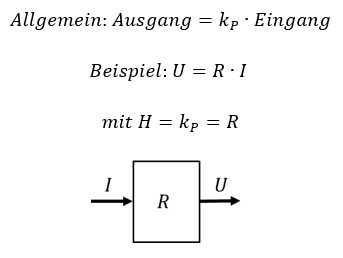
Wie bestimmen wir beim Widerstand kP bzw. R? Indem wir bei irgendeiner Spannung den Strom messen. Diese Werte setzen wir dann in die allgemeine Gleichung ein und erhalten den speziellen Wert unseres Widerstands R.
Beispiel Getriebe
Ein Getriebe verhält sich ebenfalls proportional. Der Eingang des Getriebes ist die Drehzahl N1 an Achse 1 und der Ausgang ist die Drehzahl N2 an Achse 2.
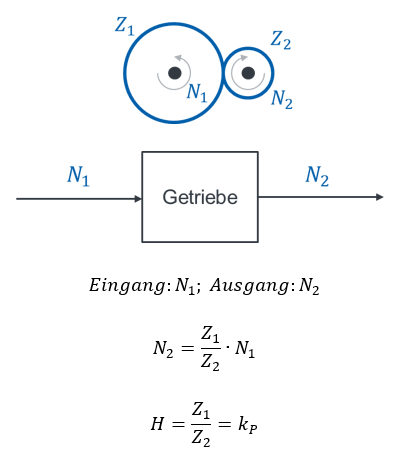
Dreht sich im Getriebe Achse 1 nicht (Eingangsgröße = 0), dreht Achse 2 auch nicht (Ausgangsgröße = 0). Je schneller Achse 1 dreht, desto schneller dreht auch Achse 2. Wie bestimmen wir kP? Entweder zählen wir die Zähne der beteiligten Zahnräder. Dann bestimmen wir kP aus dem inneren Aufbau des Getriebes. Oder wir drehen am Eingang und messen die Drehzahl am Ausgang. Dann bestimmen wir kP von außen, ohne dass wir in das Getriebe hineinschauen müssen.
Beispiel Hebel
Ein weiteres proportionales System ist der Hebel. Eingangs- und Ausgangsgrößen sind jeweils die Höhen der Endpunkte des Hebels. Wird die Höhe h1 als Eingang verändert, dann ändert sich auch die Höhe h2 aus Ausgang. Die Längen der beiden Arme des Hebels bestimmen die Steigung m bzw. die Übertragungsfunktion H des Systems.
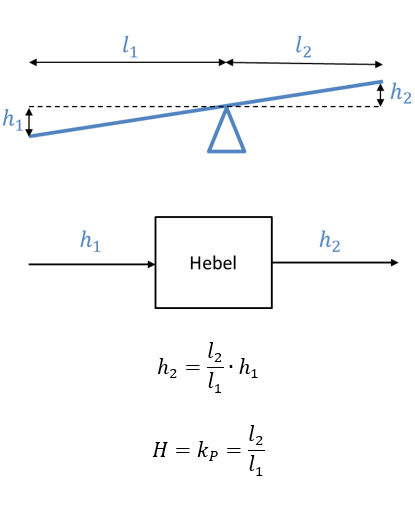
Nehmen wir als Beispiel an, die Längen betragen l1 = 40cm und l2 = 30cm, dann kann dieses System mit H = kp = 30cm / 40cm = 0,75 beschrieben werden. Wenn der Eingang von h1 = 0cm auf h1 = 10cm bewegt, dann folgt der Ausgang von h2 = 0cm auf h2 = kp ∙ 10cm = 7,5cm.
Ausnutzen der Ähnlichkeit
Widerstand, Hebel und Getriebe verhalten sich ähnlich. Alle drei Systeme können mit der gleichen Mathematik berechnet werden. Sie werden in der Regelungstechnik also auf die gleiche Weise behandelt.
Wir investieren zunächst in eine allgemeine Lösung aller Systeme mit P-Verhalten. Die allgemeine Lösung beinhaltet den charakteristischen Parameter kP.
Dann betrachten wir das spezielle System und definieren dessen Eingangs- und Ausgangsgröße. Der charakteristische Parameter kP wird für das spezielle System bestimmt. Parameter kP bestimmen wir entweder durch Messung von Eingang und Ausgang oder durch innere Größen. Mit Eingangsgröße, Ausgangsgröße und charakteristischem Parameter haben wir die allgemeine Lösung auf eine spezielle Lösung eines konkreten Problems übertragen.
Interpretation von kP
Ein Eingangssignal wird durch einen Funktionsblock mit P-Verhalten um kP verstärkt. Die Verstärkung eines Signals kann größer als 1 sein. Dann ist der Wert des Ausgangssignals größer als der des Eingangssignals. Die Verstärkung eines Signals kann gleich 1 sein. Dann wird das Signal durch den Block nicht verändert, sein Wert ist am Ausgang also gleich dem am Eingang.
Die Verstärkung eines Signals kann zwischen 0 und 1 liegen. Dann wird das Signal gedämpft, sein Wert ist am Ausgang also kleiner als am Eingang. Ist die Verstärkung gleich 0, wird am Ausgang kein Signal ausgegeben. Ist das Signal kleiner als 0, wird das Signal invertiert, sein Vorzeichen geändert sich dann zusätzlich zum Zahlenwert durch den Block. Der Wert von kp weist i. A. eine Einheit auf, wenn Eingangs- und Ausgangsgröße nicht zufällig die gleiche Einheit haben.
