Sie lernen in der Schulzeit sehr viele Formeln kennen. Dabei erklärt Ihnen Ihr Lehrer einen Zusammenhang und am Ende gibt es eine Formel für Sie. Ihr Lehrer ist dann glücklich. Viele Youtube-Videos zu technischen Themen arbeiten genauso: Auf eine sehr schwache Erklärung eines Zusammenhangs folgt die Formel, so als ob diese das Ziel einer Erklärung wäre.
Eine Formel ist für sich alleine wertlos. Erst in einem technischen Zusammenhang und wenn man sie wirklich braucht macht sie Sinn. Formeln sind wichtig, um die Welt um uns herum mathematisch zu beschreiben. Heute sind aber alle Zusammenhänge, zu denen Sie in Ihrem Studium rechnen, bereits mit Formeln beschrieben. Die Mathematik ist viel weiter als Sie das für Ihre Formeln benötigen. Sie können jede Formel jederzeit nachschlagen. Warum also sind Formeln (immer noch) das Ziel am Ende einer Erklärung?
Formeln definieren einen Zusammenhang mit Hilfe der Mathematik in Form einer Gleichung. Aus einer Gleichung können wir viel über den Zusammenhang aussagen. Zunächst beinhaltet sie ein Gleichheitszeichen, also sind beide Seiten der Gleichung gleich groß. Wenn wir auf der linken Seite des Gleichheitszeichens einen größeren Wert benötigen, müssen wir auf der rechten Seite ebenfalls einen größeren Wert einsetzen. Es gilt z. B. 2 = 2, das ist eine wahre Aussage. Erhöhen wir die linke Seite auf 3, dann gibt es nur eine wahre Aussage dazu: 3 = 3. Auch die rechte Seite muss um den gleichen Wert erhöht werden.
Liegt eine Formel in der Form
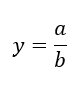
vor, kann y erhöht werden, wenn a größer wird oder wenn b kleiner wird. Ob eine Größe im Zähler oder Nenner steht ist immer wichtig. Wenn y kleiner werden soll, muss entweder b größer werden oder a muss kleiner werden. Die Formel zeigt also auch, wie eine Größe wirkt. Größen im Zähler erhöhen den Zahlenwert. Größen im Nenner reduzieren den Zahlenwert.
Für ein Wasserkraftwerk als Pumpspeicherwerk wird Wasser nachts einen Bergsee heraufgepumpt. Am Tag fließt das Wasser durch die Turbinen wieder in den See im Tal. Am Tag wird eine Energie von W = 1MWh benötigt. Sie sollen diese Anlage planen. Wie gehen Sie vor?
Sie stellen schnell fest, dass Sie zum Auslegen Formeln brauchen. Also suchen Sie nach Formeln für die Energie. Sie finden im Internet viele Formeln:
1. Thermische Energie WTHE=…
2. Kinetische Energie WKIN=…
3. Potentielle Energie WPOT=…
4. Elektrische Energie WEL=…
5. Chemische Energie WCH=…
und vieles mehr …
Zu allen Energieformen finden Sie Artikel und Formeln. Es gibt offenbar nicht die eine Formel, mit der Energie berechnet werden kann. Jede Formel ist immer nur für eine bestimmte Art der Energie, dann noch nur für einen bestimmten Zusammenhang oder Kontext gültig. Oft werden Formeln für eine bestimmte Geometrie in der Anwendung beschrieben, und schon ein etwas anderer Aufbau bekommt eine andere Formel. Die Kunst liegt also nicht im Berechnen eines Ergebnisses mit einer Formel, das können Apps bald auch alleine ohne Sie. Die Herausforderung liegt im Finden der richtigen Formel für Ihre Anwendung.
Betrachten wir dafür die potentielle Energie. Sie beschreibt, eine Energie, die von der Gravitationskraft, also der Erdanziehungskraft, bestimmt wird. Um Wasser hochzupumpen oder zu berechnen, wie viel Energie beim hinabfließen frei wird, ist diese Energieform wichtig. Schauen wir uns diese als Beispiel einmal näher an. Setzen wir dabei mal die Brille eines Ingenieurs auf, der nicht nur Zahlen einsetzt und ein Ergebnis ausrechnet, sondern der die Formel versteht.
Es gilt allgemein für mechanische Energieformen, bei denen eine Kraft entlang eines Wegs wirkt,
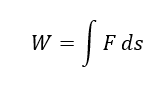
Anschaulich betrachtet müssen wir Energie investieren, um einen Gegenstand hochzuheben. Es wird Energie z. B. für eine eigenständige Bewegung frei, wenn der Gegenstand herunterfällt. Hier wirkt also eine Kraft entlang eines Wegs, und der Weg ist die Höhenänderung h. Es gilt
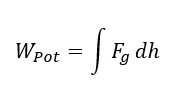
Die Gravitationskraft können wir mit der Formel Fg = m ∙ g beschreiben. Diese ist im Kontext gültig, dass Massen in einem Gravitationsfeld entlang der Feldlinien des Felds bewegt werden. Die Feldstärke g hat auf der Erdoberfläche den konstanten Wert
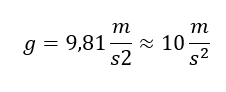
Auf dem Mond ist der Wert von g kleiner, auf der Sonne größer, er hängt von der Planetenmasse ab. Entfernen wir uns von der Erde, sinkt der Wert von g ebenfalls, er ist abhängig vom Abstand zum Zentrum des Planeten. Man muss im Zweifel viel nachlesen, um diese vermeintlich einfache Formel richtig anzuwenden. Wird die Gravitationskraft eingesetzt, gilt
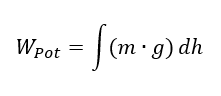
Die Parameter m und g sind unabhängig von der Höhe h. Deshalb kann das Integral vereinfacht werden zu WPOT = m ∙ g ∙ h. Das Lösen einer realen Aufgabe ist anders als das Lösen einer Klausuraufgabe. Für beides werden Formeln genutzt. Nutzen Sie bereits Ihr Studium dazu, Formeln zu hinterfragen, mit denen man vermeindlich ein Problem berechnen kann.
Wie gehen Sie im Studium mit Formeln richtig um?
1. Sie dürfen in der Klausur oft einen Formelzettel nutzen. Vermerken Sie darauf jeweils zu den Formeln den Kontext, in denen sie gültig sind, damit Sie in der Klausur die richtige Formel nutzen.
2. Wenn Sie verstehen, was passiert, wenn die Parameter der Formel sich ändern, dann können Sie einschätzen, ob Sie die richtige Formel für das Problem haben. Wenn Sie für das Auslegen des Pumpspeicherwerks Energie-Formeln mit Temperatur, Ladung oder Strahlungsintensität als Parameter ermitteln, dann beschreiben diese offensichtlich nicht ihr Problem. Recherchieren Sie mögliche gültige Formeln, bekommen Sie ein Gespür für die Parameter der Formel und deren Wirkung in der Formel und stellen Sie damit sicher, dass Sie die richtige Formel erwischt haben.
3. Prüfen Sie, für welche Geometrie die Formel gilt. Möglicherweise gibt es eine spezielle Formel für Ihre Geometrie.
4. Setzen Sie niemals ohne Nachzudenken Zahlen in eine Formel ein und erklären Sie dann das Ergebnis für gültig.
Weiter