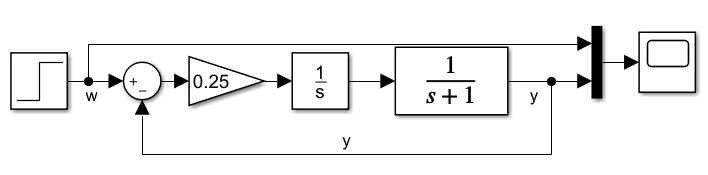
Bei schwingfähigem PT-2 Verhalten kann der Nenner der Übertragungsfunktion zu 0 werden. Als Beispiel nehmen wir ein System mit PT-1 Verhalten, das von einem I-Regler geregelt wird.
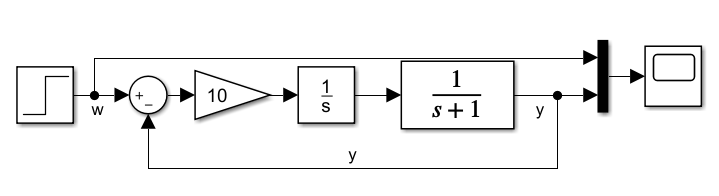
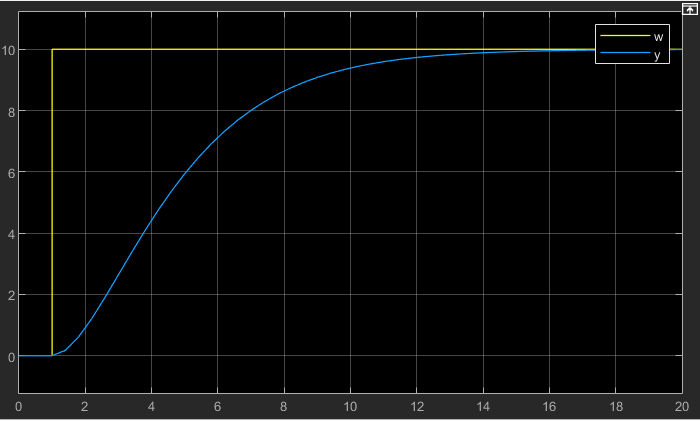
Der Parameter KI = 10 bildet zusammen mit dem Integrator 1/s den Regler. Das System ist mit einem PT-1 Block mit KPS = 1 und τ = 1 modelliert. Die Sprungantwort zeigt typisches PT-2 Verhalten. Die Regelgröße schwingt über die Führungsgröße hinaus und pendelt dann um den Wert der Führungsgrößer herum. Die Schwingung ist abklingend, bis irgendwann die Regelgröße den Wert der Führungsgröße erreicht.
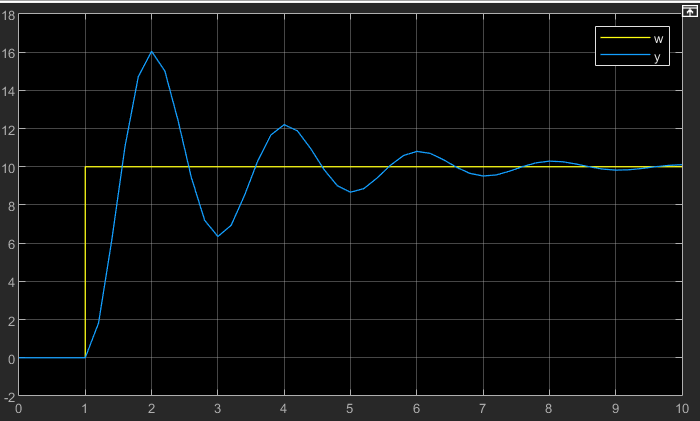
Die Mathematik hinter diesem Verhalten sieht folgendermaßen aus:
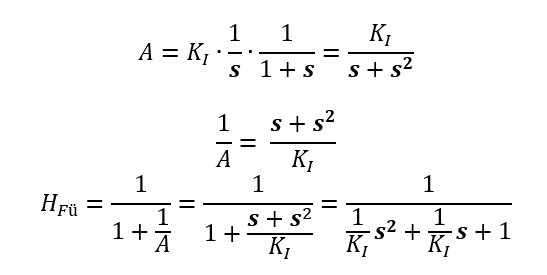
Die allgemeine Übertragungsfunktion eines schwingfähigen PT-2 Verhaltens lautet
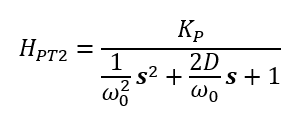
Der charakteristische Parameter ω0 gibt die Kreisfrequenz der Schwingung an. Der Koeffizientenvergleich ergibt ω02=KI. Dafür werden die Terme vor dem s2 aus der allgemeinen Formel und der Formel des konkreten Systems verglichen. Bestimmen wir also die Parameter der allgemeinen Übertragungsfunktion:
Im eingeschwungenen Zustand erreicht die Regelgröße die Führungsgröße zu 100%, siehe Sprungantwort. Für s = 0 muss also gelten HFü = 1. Das gilt für KP = 1.
Aus der Sprungantwort ermitteln wir schrittweise die Schwing-Kreisfrequenz. Die Regelgröße schwingt mit einer Periodendauer TSchwingung = 2. Das habe ich aus der Sprungantwort abgelesen. Einheiten kennt Simulink nicht, ich habe sie in Klammern ergänzt.

Da der Wert 2 für die Periodendauer nur grob abgelesen war, stimmt die Rechnung ganz gut.
Der zweite charakteristische Parameter aus der allgemeinen Formel ist die Dämpfung D. D gibt an, ob es überhaupt zu einer Schwingung kommt und wie diese ausfällt. Im Beispiel oben gilt als Gleichung für die Vorfaktoren zu s im Koeffizientenvergleich:
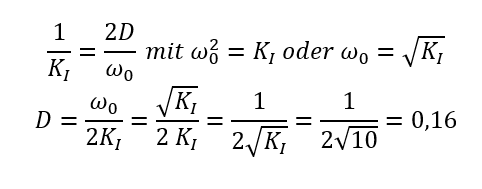
Es werden folgende Fälle unterschieden:
Es werden folgende Fälle unterschieden:
D = 0: Kontinuierliche ungedämpfte Schwingung
0 < D < 1: Abklingende Schwingung
D = 1: Aperiodischer Grenzfall
D > 1: Nicht schwingfähiges System
Mit D = 0,16 weist das System eine gedämpfte, abklingende Schwingung auf. Die Dämpfung kann aus dem Verlauf des Überschwingens ermittelt werden. Darauf gehen wir hier nicht ein, das ist mathematisch komplex.
Sie können durch Änderung des Parameters KI das Verhalten des Systems ändern. Mit größerem KI sinkt die Dämpfung und die Schwingfrequenz steigt. Das zeigt folgende Simulation für KI = 100:
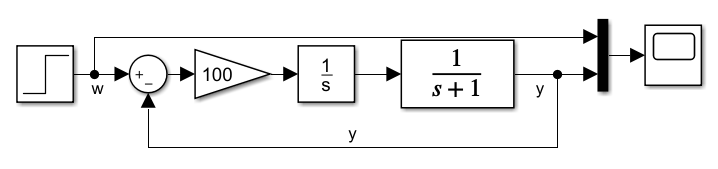
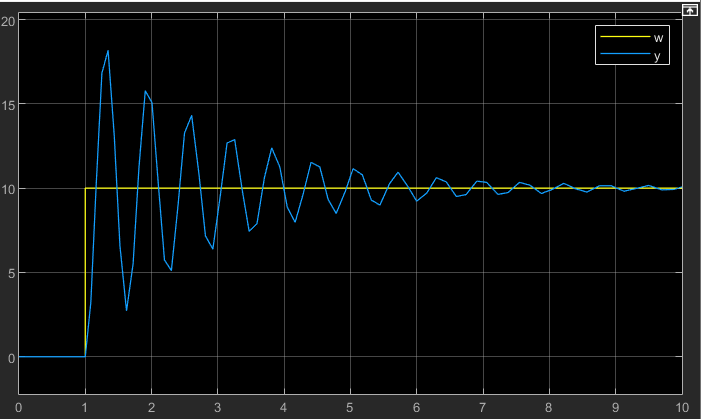
Der Begriff „Überschwingen“ gibt an, wie weit die Regelgröße über die Führungsgröße hinausschießt. Überschwingen ist in Regelkreisen oft problematisch, weil Komponenten bei zu hohem Überschwingen kurzzeitig stärker belastet werden als geplant und evtl. beschädigt werden.
Der Aperiodische Grenzfall mit D = 1 wird oft angestrebt, weil er den schnellsten möglichen Anstieg der Regelgröße ohne Überschwingen darstellt. Wenn ein Ziel für einen Regelkreis lautet, dass die Regelgröße nicht überschwingen darf, er aber möglichst schnell eingeschwungen sein soll, dann folgt daraus die Anforderung D = 1. Mit dem Beispielsystem brauchen wir dafür
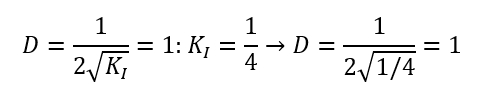
In der Sprungantwort ist die Simulationsdauer auf 20 verdoppelt worden. Die Zeit, bis das System den eingeschwungen Zustand erreicht, ist bei größerer Dämpfung (D = 1 statt D = 0,16) deutlich größer geworden. Die Zeit wird kleiner, wenn D reduziert wird.
Eine kurze Einschwingdauer ist oft erwünscht.
Aus der Sprungantwort mit D > 1 können Sie nicht mehr so einfach Informationen über Dämpfung und Schwingfrequenz ermitteln, denn es schwingt ja nichts mehr. Hier nutzen Sie die Methoden aus dem letzten Kapitel.
Es gibt bei der Auslegung eines Reglers einen Zielkonflikt. Eine kleine Dämpfung sorgt für schnelles Einschwingen, führt aber auch zu Überschwingen und (hoffentlich) abklingendem Schwingen.
Die kontinuierlich ungedämpfte Dauerschwingung mit D = 0 erreichen Sie mit der Reihenschaltung aus einem I-Regler mit einem I-System in einem Regelkreis. Dieser Fall ist weiter oben für die Erklärung von Schwingenden Systemen bereits diskutiert worden.
Erweiterung der Ziele
Für einen Regelkreis werden die Ziele folgendermaßen erweitert:
1. Es sollte gelten: HFü = 1
2. Es sollte gelten: HSu = 0
3. Das System sollte nach möglichst geringer Zeit eingeschwungen sein, also seinen Endwert erreicht haben.
4. Das Überschwingen soll auf einen maximalen Wert begrenzt werden. Das System soll nicht dauerhaft schwingen.
Weiter