Bei einem nicht schwingfähigen PT-2 Verhalten kann der Nenner der Übertragungsfunktion mathematisch nicht 0 werden. Sie entstehen oft aus dem Produkt zweier PT-1 Funktionsblöcke. Im folgenden Beispiel werden zwei PT-1 Blöcke mit τ = 1 und Kp = 1 hintereinandergeschaltet:
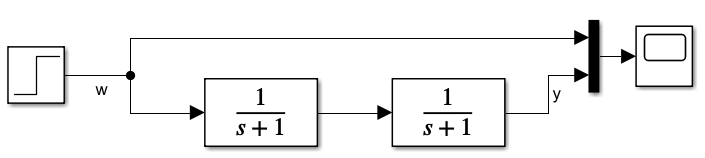
Berechnen wir zunächst die Übertragungsfunktion vom Eingang zum Ausgang. Das System ist nicht Teil eines Regelkreises, deshalb lautet die Übertragungsfunktion ganz einfach:
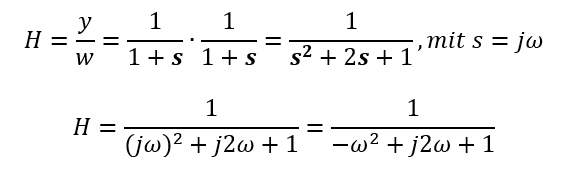
Der Nenner kann nicht 0 werden, denn entweder wird nur der Realteil zu 0 für ω = 1 oder es wird nur der Imaginärteil zu 0 für ω = 0. Beides geht nicht. Die Sprungantwort sieht folgendermaßen aus:
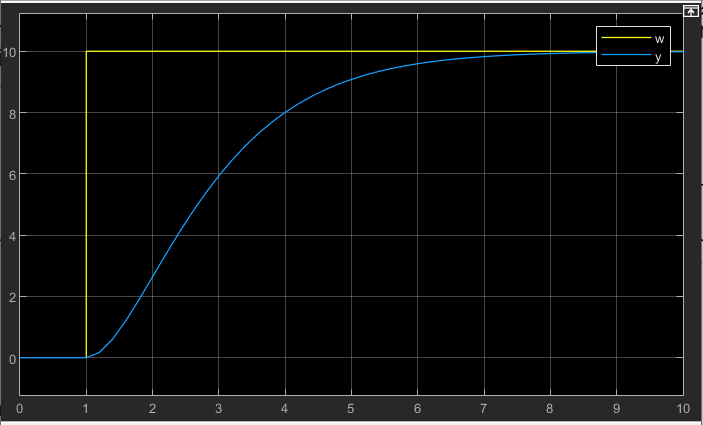
PT-1 Verhalten und nicht schwingfähiges PT-2 Verhalten können in der Sprungantwort nur dadurch unterschieden werden, dass beim nicht schwingfähigen PT-2 Verhalten der Ausgang direkt nach dem Sprung stetig bleibt. Es gibt keine Sprung nach oben, sondern einen weichen Übergang.
Die Parameter solcher Systeme sind aus der Sprungantwort heraus schwer zu ermitteln. Dafür bietet sich z. B. das Wendetangentenverfahren an, das aus der Sprungantwort charakteristische Parameter bezieht, aus denen direkt Regler-Parameter eines PID-Reglers bestimmt werden können.
Beim Wendetangenten-Verfahren zeichnen Sie in den Wendepunkt der Sprungantwort eine Tangente. Sie können am Bildschirm auch ein Lineal als Tangente anlegen. Aus der Grafik ermitteln Sie die beiden Zeiten tu und tg so wie in der folgenden Abbildung:
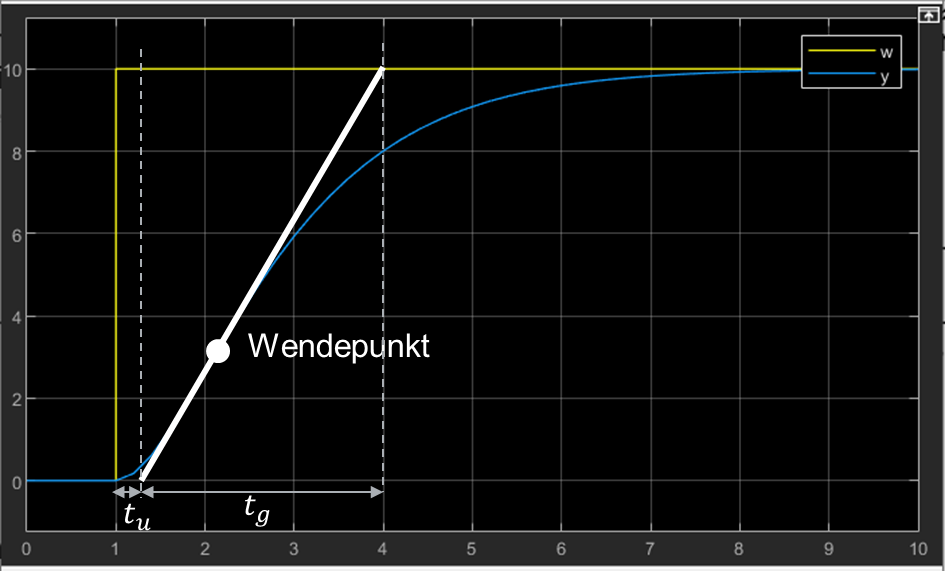
tu ist die Zeit zwischen dem Sprung am Eingang und dem Schnittpunkt der Wendetangente mit der Null-Linie. tg ist die Zeit zwischen Schnittpunkt der Wendetangente mit der Null-Linie und Schnittpunkt der Wendetangente mit dem verlängerten statischen Endwert des Ausgangswerts.
Es gibt Tabellen, aus denen direkt Regler-Parameter entnommen werden können, die aus den beiden Zeiten abgeleitet werden. Das wird hier nicht weiter vertieft. Das Verfahren ist sehr ungenau, denn den Wendepunkt genau zu treffen ist schwierig. Leichte Verschiebungen des Wendepunkts führen schnell zu großen Abweichungen in den ermittelten Zeiten. Die mit diesem Verfahren ermittelten Regelparameter sind nur ein Startwert für weitere Optimierungen. Leider gibt es kein wirklich gut geeignetes Verfahren zur Charakterisierung eines solchen nicht schwingfähigen PT-2 Verhaltens.
Nicht schwingfähiges PT-2 Verhalten wird üblicherweise über die Parameter tu und tg charakterisiert.
Als nächstes betrachten wir Schwingungen in Systemen mit PT-2 Verhalten.
Weiter